题目内容
14.已知函数f(x)=loga(x+1)(a>1),若函数y=g(x)的图象上任意一点P关于原点的对称点Q的轨迹恰好是函数f(x)的图象(1)写出函数y=g(x)的解析式;
(2)求不等式2f(x)+g(x)≥0的解集A;
(3)当x∈A时,总有f(x)+g(x)≥m成立,求m的取值范围.
分析 (1)把函数称问题转化为点的对称:P(x,y)在函数y=g(x)的图象上,则Q(-x,-y)在函数f(x)的图象,y=g(x),得出-y=f(-x),y=-log(1-x),即可求解g(x)的图象.
(2)2loga(x+1)-loga(1-x)≥0,利用对数函数的单调性求解即可
(3)分离参数得出:m≤loga$\frac{1+x}{1-x}$恒成立,转化为求函数y=loga$\frac{1+x}{1-x}$在[0,1)的值域问题.
解答 解:(1)∵函数f(x)=loga(x+1)(a>1),
函数y=g(x)的图象上任意一点P关于原点的对称点Q的轨迹恰好是函数f(x)的图象.
∴设P(x,y)在函数y=g(x)的图象上,则Q(-x,-y)在函数f(x)的图象,y=g(x)
∴-y=f(-x),y=-log(1-x),
g(x)=-loga(1-x)
(2)2loga(x+1)-loga(1-x)≥0,a>1,
$\left\{\begin{array}{l}{lo{g}_{a}\frac{(1+x)^{2}}{1-x}≥0}\\{-1<x<1}\end{array}\right.$,得解集[0,1)
(3)loga(x+1)-loga(1-x)≥m恒成立
即m≤loga$\frac{1+x}{1-x}$恒成立,函数y=loga$\frac{1+x}{1-x}$在[0,1)上值域[0,+∞)
所以m≤0.
点评 本题考查了对数函数的单调性,不等式,分离参数问题,考查了学生的综合解决问的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.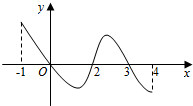 已知函数f(x)的定义域为[-1,4],部分对应值如表,
已知函数f(x)的定义域为[-1,4],部分对应值如表,
f(x)的导函数y=f′(x)的图象如图所示.当1<a<2时,函数y=f(x)-a的零点的个数为( )
 已知函数f(x)的定义域为[-1,4],部分对应值如表,
已知函数f(x)的定义域为[-1,4],部分对应值如表,| x | -1 | 0 | 2 | 3 | 4 |
| f(x) | 1 | 2 | 0 | 2 | 0 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.设复数$z=\frac{2}{-1-i}$,则$z•\overline z$=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
3.如图所示,在正方形OABC中任取一点,则该点落在阴影部分的概率为( )
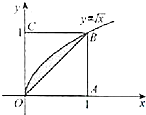

| A. | $\frac{1}{7}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{4}$ |
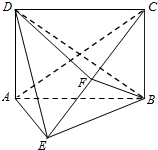 如图,在四棱锥E-ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,
如图,在四棱锥E-ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,