题目内容
14.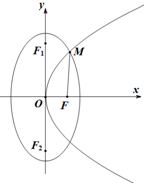 如图,抛物线C1:y2=2px(p>0)与椭圆C2:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{4}$=1(a>2)交于第一象限内一点M,F为抛物线C1的焦点,F1,F2分别为椭圆C2的上下焦点,已知|$\overrightarrow{MF}$-|$\overrightarrow{OF}$|=1,|$\overrightarrow{MF}$-$\overrightarrow{OF}$|=$\sqrt{10}$.
如图,抛物线C1:y2=2px(p>0)与椭圆C2:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{4}$=1(a>2)交于第一象限内一点M,F为抛物线C1的焦点,F1,F2分别为椭圆C2的上下焦点,已知|$\overrightarrow{MF}$-|$\overrightarrow{OF}$|=1,|$\overrightarrow{MF}$-$\overrightarrow{OF}$|=$\sqrt{10}$.(1)求抛物线C1和椭圆C2的方程;
(2)是否存在经过M的直线l,与抛物线和椭圆分别交于非M的两点P,Q,使得$\overrightarrow{{F}_{1}P}$+$\overrightarrow{{F}_{2}Q}$=2$\overrightarrow{OM}$?若存在请求出直线的斜率,若不存在,请说明理由.
分析 (1)求出抛物线的焦点和准线方程,运用抛物线的定义和两点的距离公式,解方程可得p,a,即可得到抛物线方程和椭圆方程;
(2)假设存在经过M的直线l,与抛物线和椭圆分别交于非M的两点P,Q,使得$\overrightarrow{{F}_{1}P}$+$\overrightarrow{{F}_{2}Q}$=2$\overrightarrow{OM}$.直线的斜率不存在显然不成立,设l:y=k(x-1)+3,联立抛物线方程和椭圆方程,求得P,Q的坐标,再由向量的坐标表示,即可得到k=1,即可判断存在.
解答 解:(1)y2=2px(p>0)的焦点F($\frac{p}{2}$,0),准线方程为x=-$\frac{p}{2}$,
由|$\overrightarrow{MF}$|-|$\overrightarrow{OF}$|=1,|$\overrightarrow{MF}$-$\overrightarrow{OF}$|=$\sqrt{10}$即|$\overrightarrow{MO}$|=$\sqrt{10}$,
由题意得$\left\{\begin{array}{l}{({x}_{M}+\frac{p}{2})-\frac{p}{2}=1}\\{{{x}_{M}}^{2}+{{y}_{M}}^{2}=10}\end{array}\right.$,解得xM=1,yM=3,
分别代入抛物线和椭圆方程得:C1:y2=9x,C2:$\frac{{y}^{2}}{12}$+$\frac{{x}^{2}}{4}$=1.
(2)斜率不存在时显然不合题意,
假设存在经过M的直线l,与抛物线和椭圆分别交于非M的两点P,Q,
使得$\overrightarrow{{F}_{1}P}$+$\overrightarrow{{F}_{2}Q}$=2$\overrightarrow{OM}$.
由M(1,3),可设l:y=k(x-1)+3,
直线与抛物线联立得:k2x2+(-2k2+6k-9)x+(3-k)2=0,
由韦达定理可得xM+xP=$\frac{2{k}^{2}-6k+9}{{k}^{2}}$,
及xM=1可得xP=$\frac{(3-k)^{2}}{{k}^{2}}$;
直线与椭圆联立得:(3+k2)x2+2k(3-k)x+(k2-6k-3)=0,
由韦达定理可得xM•xQ=$\frac{{k}^{2}-6k-3}{3+{k}^{2}}$.
及xM=1可得xQ=$\frac{{k}^{2}-6k-3}{3+{k}^{2}}$.
由$\overrightarrow{{F}_{1}P}$+$\overrightarrow{{F}_{2}Q}$=2$\overrightarrow{OM}$可得xP+xQ=2xM,可得4k3-k2+6k-9=0,
可得(k-1)(4k2+3k+9)=0,
解得k=1,经检验符合题意.
则存在符合题意的直线,其斜率为1.
点评 本题考查抛物线的定义、方程和性质,同时考查椭圆的方程的运用,注意联立直线方程和曲线方程,运用韦达定理,考查向量的坐标表示,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 0 | B. | 1 | C. | 3 | D. | 4 |