题目内容
13．在直角坐标系xoy中，曲线C1的参数方程为$\left\{\begin{array}{l}x=cosa\\ y=sina\end{array}\right.$（a为参数），以原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρsinθ=4．设P为曲线C1上的动点，则点P到C2上点的距离的最小值为3．分析 把曲线C1的参数方程化为普通方程是单位圆，把曲线C2的极坐标方程化为普通方程是直线y=4，
利用圆心到直线的距离求出曲线C1上的点到直线的最小距离．
解答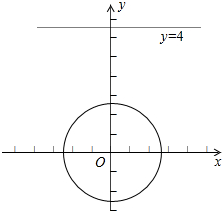 
解：曲线C1的参数方程为$\left\{\begin{array}{l}x=cosa\\ y=sina\end{array}\right.$（a为参数），
消去参数α，化为普通方程是x2+y2=1；
又曲线C2的极坐标方程为ρsinθ=4，
化为普通方程是y=4；
如图所示，
圆心O到直线y=4的距离是d=4；
所以，曲线C1上的动点P到直线y=4的最小距离为3．
故答案为：3．
点评 本题考查了直线与圆的应用问题，也考查了参数方程与极坐标的应用问题，解题时应把参数方程与极坐标化为普通方程，是基础题目．
练习册系列答案
相关题目
3．如图所示，在正方形OABC中任取一点，则该点落在阴影部分的概率为（ ）
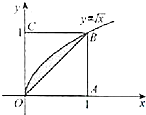
| A． | $\frac{1}{7}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{5}$ | D． | $\frac{1}{4}$ |
1．
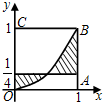如图，正方形OABC的边长为1，记曲线y=x2和直线$y=\frac{1}{4}$，x=1，x=0所围成的图形（阴影部分）为Ω，若向正方形OABC内任意投一点M，则点M落在区域Ω内的概率为（ ）
如图，正方形OABC的边长为1，记曲线y=x2和直线$y=\frac{1}{4}$，x=1，x=0所围成的图形（阴影部分）为Ω，若向正方形OABC内任意投一点M，则点M落在区域Ω内的概率为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{2}{5}$ |
18．已知复数z=1+i+i2+…i10，则复数z在复平面内对应的点为（ ）
| A． | （1，1） | B． | （1，-1） | C． | （0，1） | D． | （1，0） |