题目内容

16．已知函数f（x）=aln（1+x）-aln（1-x）-x-$\frac{{x}^{3}}{3（1-{x}^{2}）}$．当0＜x＜1时，f（x）＜0，求实数a的取值范围．

分析 求导数，利用判别式分类讨论，结合函数的单调性，即可求实数a的取值范围；

解答 解：f′（x）=$\frac{-2{x}^{4}+（3-6a）{x}^{2}+6a-3}{3（1-{x}^{2}）^{2}}$，
依题知f（0）=0，故f′（x）≤0，则a≤$\frac{1}{2}$．
令g（x）=-2x2+（3-6a）x+6a-3，x∈（0，1]，△=（6a-3）（6a+5）
①-$\frac{5}{6}≤a≤$$\frac{1}{2}$，△≤0，此时g（x）≤0，故f′（x）≤0，而f（0）=0，所以-$\frac{5}{6}≤a≤$$\frac{1}{2}$符合题意．
②a＜-$\frac{5}{6}$，△＞0，而g（x）对称轴x=$\frac{3-6a}{4}$＞2，故g（x）在（0，1）单调递增
且g（1）=-2，则g（x）＜0，故f′（x）≤0，而f（0）=0，所以a＜-$\frac{5}{6}$符合题意．
综上，a≤$\frac{1}{2}$．

点评 本题考查导数知识的综合运用，考查函数的单调性，考查不等式的证明，正确运用导数的关键．属于中档题目．

练习册系列答案
相关题目
6．设复数$z=\frac{2}{-1-i}$，则$z•\overline z$=（　　）
A．1B．$\sqrt{2}$C．2D．4
7．在平面直角坐标系中，实数x，y满足$\left\{\begin{array}{l}x+y-1≥0\\ x-1≤0\\ x-y+1≥0\end{array}\right.$，若z=-2x+y，则z的取值范围是[-2，1]．
4．已知函数f（x）=$\frac{1}{2}$x2-ax+（a-1）lnx（a＞1）．
（Ⅰ） 讨论函数f（x）的单调性；
（Ⅱ） 若a=2，数列{an}满足an+1=f（an）．
（1）若首项a1=10，证明数列{an}为递增数列；
（2）若首项为正整数，且数列{an}为递增数列，求首项a1的最小值．
11．已知直线l1：y=kx+1和直线l2：y=mx+m，则“k=m”是“l1∥l2”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
1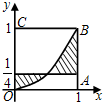．如图，正方形OABC的边长为1，记曲线y=x2和直线$y=\frac{1}{4}$，x=1，x=0所围成的图形（阴影部分）为Ω，若向正方形OABC内任意投一点M，则点M落在区域Ω内的概率为（　　）
A．$\frac{1}{4}$B．$\frac{1}{3}$C．$\frac{2}{3}$D．$\frac{2}{5}$
8．已知函数f（x）=ln（1+x）（x＞0）．
（Ⅰ）证明：$\frac{x}{1+x}＜f（x）$；
（Ⅱ）比较20152013与20142014的大小；
（Ⅲ）给定正整数n（n＞2015），n个正实数x1，x2，…，xn满足x1+x2+…+xn=1，
证明：${（\frac{{{x_1}^2}}{{1+{x_1}}}+\frac{{{x_2}^2}}{{1+{x_2}}}+…+\frac{{{x_n}^2}}{{1+{x_n}}}）^{2015}}＞{（\frac{1}{2016}）^n}$．
5．设集合A=[-2，4），B={x|x2-ax-4≤0}，若B⊆A，则实数a的取值范围是[0，3）．
6．在（x2+$\frac{4}{x^2}$-4）5的展开式中含x4项的系数是-960．（用数字填写答案）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网