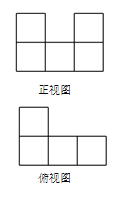
题目内容
【题目】在无穷数列![]() 中,
中, ![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,
, ![]() .设
.设![]() ,记使得
,记使得![]() 成立的n的最大值为
成立的n的最大值为![]() .
.
(Ⅰ)设数列{an}为1,3,5,7,…,写出b1,b2,b3的值;
(Ⅱ)若{an}为等比数列,且a2=2,求b1+b2+b3+…+b50的值;
(Ⅲ)若{bn}为等差数列,求出所有可能的数列{an}.
【答案】(Ⅰ)b1=1, b2=1, b3=2;(Ⅱ)243;(Ⅲ) ![]() .
.
【解析】试题分析:
(Ⅰ)由题意结合数列![]() 的定义可得b1=1, b2=1, b3=2.
的定义可得b1=1, b2=1, b3=2.
(Ⅱ)由题意可得![]() ,则b1=1,b2=b3=2,b4=b5= b6= b7=3,b8=b9
,则b1=1,b2=b3=2,b4=b5= b6= b7=3,b8=b9![]() b15=4,b16=b17
b15=4,b16=b17![]() b31=5,b32=b33
b31=5,b32=b33![]() b50= 6.故b1+ b2+b3
b50= 6.故b1+ b2+b3![]() b50=243.
b50=243.
(Ⅲ)由题意可知![]() .使得
.使得![]() 成立的n的最大值为
成立的n的最大值为![]() ,使得
,使得![]() 成立的n的最大值为
成立的n的最大值为![]() ,则
,则![]() .结合题中的条件分析可得
.结合题中的条件分析可得![]() ,故
,故![]() .
.
试题解析:
(Ⅰ)b1=1, b2=1, b3=2.
(Ⅱ)因为![]() 为等比数列, a1=1,a2=2,
为等比数列, a1=1,a2=2,
所以![]() ,
,
因为使得an≤m成立的n的最大值为bm,
所以b1=1,b2=b3=2,b4=b5= b6= b7=3,b8=b9![]() b15=4,b16=b17
b15=4,b16=b17![]() b31=5,b32=b33
b31=5,b32=b33![]() b50= 6.故b1+ b2+b3
b50= 6.故b1+ b2+b3![]() b50=243.所以b1+ b2+b3+…b50=243.
b50=243.所以b1+ b2+b3+…b50=243.
(Ⅲ)由题意,得![]() ,
,
结合条件![]() ,得
,得![]() .
.
又因为使得![]() 成立的n的最大值为
成立的n的最大值为![]() ,使得
,使得![]() 成立的n的最大值为
成立的n的最大值为![]() ,所以
,所以![]() ,
, ![]() .设
.设![]() ,则
,则![]() .
.
假设![]() ,即
,即![]() ,则当
,则当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以![]() ,
, ![]() .
.
因为![]() 为等差数列,所以公差
为等差数列,所以公差![]() ,所以
,所以![]() ,其中
,其中![]() .
.
这与![]() (
(![]() )矛盾,所以
)矛盾,所以![]() .
.
又因为![]() ,所以
,所以![]() ,
,
由![]() 为等差数列,得
为等差数列,得![]() ,其中
,其中![]() .
.
因为使得![]() ,由
,由![]() ,
,
得![]() .
.
(1)本题解题的关键是抓住新定义中使得![]() 成立的n的最大值为
成立的n的最大值为![]() ,可将问题迎刃而解.
,可将问题迎刃而解.
(2)对于这类问题,我们首先应弄清问题的本质,然后根据等差数列、等比数列的性质以及解决数列问题时常用的方法即可解决.

 阅读快车系列答案
阅读快车系列答案【题目】为了调查喜欢旅游是否与性别有关,调查人员就“是否喜欢旅游”这个问题,在火车站分别随机调研了 ![]() 名女性或
名女性或 ![]() 名男性,根据调研结果得到如图所示的等高条形图.
名男性,根据调研结果得到如图所示的等高条形图.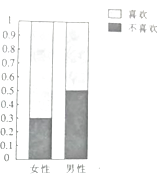
(1)完成下列 ![]() 列联表:
列联表:
喜欢旅游 | 不喜欢旅游 | 估计 | |
女性 | |||
男性 | |||
合计 |
(2)能否在犯错误概率不超过 ![]() 的前提下认为“喜欢旅游与性别有关”.
的前提下认为“喜欢旅游与性别有关”.
附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:![]() ,其中
,其中 ![]()
【题目】假设关于某种设备的使用年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有如下统计资料:
(万元)有如下统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
.
 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2) ![]() 与
与![]() 具有线性相关关系,求出线性回归方程;
具有线性相关关系,求出线性回归方程;
(3)估计使用年限为10年时,维修费用约是多少?