题目内容
【题目】如图1,△ABC是等腰直角三角形∠CAB=90°,AC=2a,E,F分别为AC,BC的中点,沿EF将△CEF折起,得到如图2所示的四棱锥C′﹣ABFE
(1)求证:AB⊥平面AEC′;
(2)当四棱锥C′﹣ABFE体积取最大值时,
①若G为BC′中点,求异面直线GF与AC′所成角;
②在C′﹣ABFE中AE交BF于C,求二面角A﹣CC′﹣B的余弦值.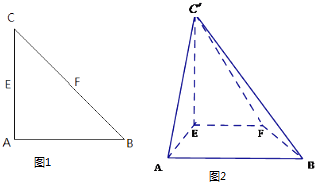
【答案】
(1)解:证明:因为△ABC 是等腰直角三角形,∠CAB=90°,E,F 分别为AC,BC 的中点,
所以EF⊥AE,EF⊥C'E.
又因为AE∩C'E=E,所以EF⊥平面AEC'.
由于EF∥AB,所以有AB⊥平面AEC'.
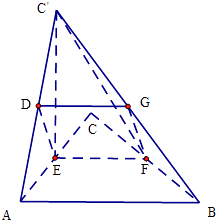
(2)解:①取AC'中点D,连接DE,EF,FG,GD,
由于GD 为△ABC'中位线,以及EF 为△ABC 中位线,
所以四边形DEFG 为平行四边形.
直线GF 与AC'所成角就是DE 与AC'所成角.
所以四棱锥C'﹣ABFE 体积取最大值时,C'E 垂直于底面ABFE.
此时△AEC'为等腰直角三角形,
ED 为中线,所以直线ED⊥AC'.
又因为ED∥GF,所以直线GF 与AC'所成角为 ![]() .
.
② 因为四棱锥C'﹣ABFE 体积取最大值,
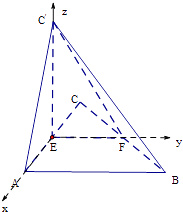
分别以EA、EF、EC'所在直线为x 轴、y 轴、z 轴,建立空间直角坐标系如图,
则C'(0,0,a),B(a,2a,0),F(0,a,0),C'B(a,2a,﹣a),C'F(0,a,﹣a).
设平面C'BF 的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
由 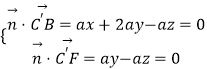 得,取y=1,得
得,取y=1,得 ![]() =(﹣1,1,1).
=(﹣1,1,1).
平面C'AE 的一个法向量 ![]() =(0,1,0).
=(0,1,0).
所以cos< ![]() >=
>= ![]() =
= ![]() ,
,
故平面C'AE与平面C'BF的平面角的夹角的余弦值为 ![]() .
.
【解析】(1)推导出EF⊥AE,EF⊥C'E,从而EF⊥平面AEC',由此能证明AB⊥平面AEC'.(2)①取AC'中点D,连接DE,EF,FG,GD,推导出四边形DEFG 为平行四边形,直线GF 与AC'所成角就是DE 与AC'所成角,由此能求出直线GF 与AC'所成角.②分别以EA、EF、EC'所在直线为x 轴、y 轴、z 轴,建立空间直角坐标系,利用向量法能求出平面C'AE与平面C'BF的平面角的夹角的余弦值.

 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
