题目内容
8.已知△ABC的三边长为a、b、c,且其中任意两边长均不相等.若$\frac{1}{a}$,$\frac{1}{b}$,$\frac{1}{c}$成等差数列.(Ⅰ)比较$\frac{b}{a}$与$\frac{c}{b}$的大小,并证明你的结论.
(Ⅱ)求证:B不可能是钝角.
分析 (Ⅰ)由条件可得$\frac{2}{b}$=$\frac{1}{a}$+$\frac{1}{c}$>2$\sqrt{\frac{1}{ac}}$,可得$\frac{b}{a}$<$\frac{c}{b}$.
(2)由条件得到b2<ac,利用基本不等式变形,可得出cosB的范围,利用余弦函数的图象与性质,以及特殊角的三角函数值,根据B为三角形的内角,即可求出B的范围.
解答 (Ⅰ)解:∵△ABC的三边长为a、b、c,且其中任意两边长均不相等,$\frac{1}{a}$,$\frac{1}{b}$,$\frac{1}{c}$成等差数列,
∴$\frac{2}{b}$=$\frac{1}{a}$+$\frac{1}{c}$>2$\sqrt{\frac{1}{ac}}$.
∴b2<ac,
∴$\frac{b}{a}$<$\frac{c}{b}$.
(Ⅱ)证明:∵b2<ac,
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$>$\frac{1}{2}$,
∴B∈[0,$\frac{π}{3}$],
∴B不可能是钝角.
点评 此题考查了余弦定理,等差、等比数列的性质,以及基本不等式的运用,熟练掌握定理及性质是解本题的关键,属于中档题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
16.复数z=$\frac{-2i}{1+i}$的虚部为( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
3.已知a=$\frac{1}{n}$$\underset{\stackrel{n}{∑}}{i=1}$($\frac{i}{n}$)2(n∈N*),b=${∫}_{0}^{1}$x2dx,则a,b的大小关系为( )
| A. | a<b | B. | a=b | ||
| C. | a>b | D. | a,b的大小与n的取值有关 |
13.边长为6的正方形ABCD的中心为O,以O为圆心2为半径作圆,点P是圆O上的任意一点,点Q是边AB,BC,CD,DA上的任意一点(含端点),则$\overrightarrow{PQ}$•$\overrightarrow{DA}$的取值范围为( )
| A. | [-40,40] | B. | [-30,30] | C. | [-15,15] | D. | [-10,10] |
17.深圳市某学校为了了解学生使用手机与学习成绩之间的关系,抽查了有手机同学40名,其中成绩为优秀的人数24名,抽查没有手机同学20人,其中成绩为优秀的人数15名,
(1)根据以上数据完成下面的2×2列联表(单位:人)
(2)根据题(1)中表格的数据计算,你有多大的把握,认为学生手机与成绩之间有关系?
(1)根据以上数据完成下面的2×2列联表(单位:人)
| 拥有手机 | 没有手机 | 合计 | |
| 成绩优秀 | |||
| 成绩不优势 | |||
| 合计 |
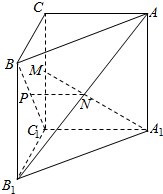 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=$\sqrt{6}$,点P、M、N分别为BC1、CC1、AB1的中点.
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=$\sqrt{6}$,点P、M、N分别为BC1、CC1、AB1的中点. 某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100],则图中a的值为0.005.
某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100],则图中a的值为0.005.