题目内容
18.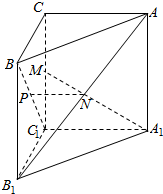 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=$\sqrt{6}$,点P、M、N分别为BC1、CC1、AB1的中点.
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=$\sqrt{6}$,点P、M、N分别为BC1、CC1、AB1的中点.(1)求证:PN∥平面ABC;
(2)求证:A1M⊥面AB1C1.
分析 (1)根据线面平行的判定定理证明即可;(2)根据线面垂直的判定定理证明即可.
解答 解(1)证明:连接CB1,QP是BC1的中点,
∴CB1过点P,
QN为AB1的中点,
∴PN∥AC,
又∵AC?面ABC,PN?面ABC,
∴PN∥平面ABC;
(2)证明:连结AC1,连接AC1,在直角△ABC中,
∵BC=1,∠BAC=30°,
∴AC=A1 C1=$\sqrt{3}$,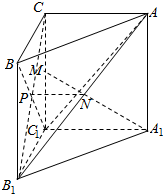
∵$\frac{{CC}_{1}}{{{A}_{1}C}_{1}}$=$\frac{{{A}_{1}C}_{1}}{{MC}_{1}}$=$\sqrt{2}$,
∴RT△A1C1M∽RT△C1CA,
∴∠AM1C1=∠CAC1,
∴∠AC1C+∠CAC1=∠AC1C+∠A1MC1=90°,
即AC1⊥A1M,
∵B1C1⊥C1A1,CC1⊥B1C1,且C1A1∩CC1=C1,
∴B1C1⊥平面AA1C1C,
∴B1C1⊥A1M,又AC1∩B1C1=C1,
故A1M⊥平面AB1C1;
点评 本题考察了线面平行、线面垂直的判定定理,是一道中档题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
8.一个角的度数是45°,化为弧度数是( )
| A. | 45 | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
9.复数ω=$\frac{3i-1}{i}$的虚部和模依次是( )
| A. | 3,2$\sqrt{2}$ | B. | 3i,$\sqrt{10}$ | C. | 1,$\sqrt{10}$ | D. | -1,2$\sqrt{2}$ |
10.已知点P(sinα-cosα,tanα)在第一象限,则在[0,2π]内α的取值范围是( )
| A. | ($\frac{π}{2}$,$\frac{3π}{4}$)∪(π,$\frac{5π}{4}$) | B. | ($\frac{π}{4}$,$\frac{π}{2}$)∪(π,$\frac{5π}{4}$) | C. | ($\frac{π}{2}$,$\frac{3π}{4}$)∪($\frac{5π}{4}$,$\frac{3π}{2}$) | D. | ($\frac{π}{4}$,$\frac{π}{2}$)∪($\frac{3π}{4}$,π) |
7.设{an}是由正数组成的等差数列,{bn}是由正数组成的等比数列,且a1=b1,a2015=b2015,则必有( )
| A. | a1008>b1008 | B. | a1008=b1008 | C. | a1008≥b1008 | D. | a1008≤b1008 |
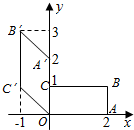 如图,矩形OABC在变换T的作用下变成了平行四边形OA′B′C′,变换T所对应的矩阵为M,矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍的变换所对应的矩阵.
如图,矩形OABC在变换T的作用下变成了平行四边形OA′B′C′,变换T所对应的矩阵为M,矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍的变换所对应的矩阵.