题目内容
设数列{an}的前n项和为Sn,数列{Sn}的前n项和为Tn,满足Tn=2Sn-n2,n∈N*.
(1)求a1的值;
(2)求数列{an}的通项公式.
(1)求a1的值;
(2)求数列{an}的通项公式.
(1)a1=1.(2)an=3·2n-1-2
(1)当n=1时,T1=2S1-12.因为T1=S1=a1,所以a1=2a1-1,解得a1=1.
(2)当n≥2时,Sn=Tn-Tn-1=2Sn-n2-[2Sn-1-
(n-1)2]=2Sn-2Sn-1-2n+1,所以Sn=2Sn-1+2n-1, ①
所以Sn+1=2Sn+2n+1,②
②-①得an+1=2an+2.
所以an+1+2=2(an+2),即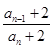 =2(n≥2). (*)
=2(n≥2). (*)
当n=1时,a1+2=3,a2+2=6,则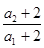 =2.
=2.
所以,当n=1时,适合(*)式,所以{an+2}是以3为首项,2为公比的等比数列.
则an+2=3·2n-1,所以an=3·2n-1-2.
(2)当n≥2时,Sn=Tn-Tn-1=2Sn-n2-[2Sn-1-
(n-1)2]=2Sn-2Sn-1-2n+1,所以Sn=2Sn-1+2n-1, ①
所以Sn+1=2Sn+2n+1,②
②-①得an+1=2an+2.
所以an+1+2=2(an+2),即
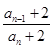 =2(n≥2). (*)
=2(n≥2). (*)当n=1时,a1+2=3,a2+2=6,则
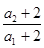 =2.
=2.所以,当n=1时,适合(*)式,所以{an+2}是以3为首项,2为公比的等比数列.
则an+2=3·2n-1,所以an=3·2n-1-2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
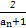 ,bn=|
,bn=| |,n∈N*,则数列{bn}的通项公式bn= .
|,n∈N*,则数列{bn}的通项公式bn= .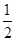 ,a6+a7=3.则满足a1+a2+…+an>a1a2…an的最大正整数n的值为________.
,a6+a7=3.则满足a1+a2+…+an>a1a2…an的最大正整数n的值为________.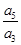
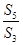


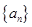 共有奇数项,所有奇数项和
共有奇数项,所有奇数项和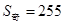 ,所有偶数项和
,所有偶数项和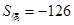 ,末项是
,末项是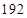 ,则首项
,则首项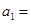 ( )
( )