题目内容
在正项等比数列{an}中,a5=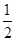 ,a6+a7=3.则满足a1+a2+…+an>a1a2…an的最大正整数n的值为________.
,a6+a7=3.则满足a1+a2+…+an>a1a2…an的最大正整数n的值为________.
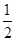 ,a6+a7=3.则满足a1+a2+…+an>a1a2…an的最大正整数n的值为________.
,a6+a7=3.则满足a1+a2+…+an>a1a2…an的最大正整数n的值为________.12
由已知条件得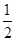 q+
q+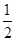 q2=3,即q2+q-6=0,解得q=2,或q=-3(舍去),an=a5qn-5=
q2=3,即q2+q-6=0,解得q=2,或q=-3(舍去),an=a5qn-5=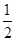 ×2n-5=2n-6,a1+a2+…+an=
×2n-5=2n-6,a1+a2+…+an=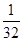 (2n-1),a1a2…an=2-52-42-3…2n-6=2
(2n-1),a1a2…an=2-52-42-3…2n-6=2 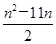 ,由a1+a2+…+an>a1a2…an,可知2n-5-2-5>2
,由a1+a2+…+an>a1a2…an,可知2n-5-2-5>2 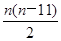 ,由2n-5>2
,由2n-5>2 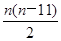 ,可求得n的最大值为12,而当n=13时,28-2-5<213,所以n的最大值为12.
,可求得n的最大值为12,而当n=13时,28-2-5<213,所以n的最大值为12.
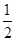 q+
q+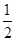 q2=3,即q2+q-6=0,解得q=2,或q=-3(舍去),an=a5qn-5=
q2=3,即q2+q-6=0,解得q=2,或q=-3(舍去),an=a5qn-5=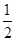 ×2n-5=2n-6,a1+a2+…+an=
×2n-5=2n-6,a1+a2+…+an=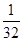 (2n-1),a1a2…an=2-52-42-3…2n-6=2
(2n-1),a1a2…an=2-52-42-3…2n-6=2 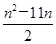 ,由a1+a2+…+an>a1a2…an,可知2n-5-2-5>2
,由a1+a2+…+an>a1a2…an,可知2n-5-2-5>2 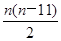 ,由2n-5>2
,由2n-5>2 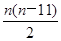 ,可求得n的最大值为12,而当n=13时,28-2-5<213,所以n的最大值为12.
,可求得n的最大值为12,而当n=13时,28-2-5<213,所以n的最大值为12.
练习册系列答案
相关题目
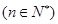 个正数
个正数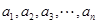 使得这
使得这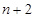 个数构成递增的等比数列,将这
个数构成递增的等比数列,将这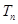 ,令
,令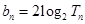 .
.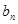 }的通项公式;
}的通项公式;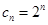 ,设
,设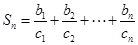 ,求
,求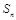 .
.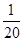 ,9S3=S6,设Tn=a1a2a3…an,则使Tn取最小值的n值为( ).
,9S3=S6,设Tn=a1a2a3…an,则使Tn取最小值的n值为( ).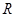 上的函数
上的函数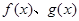 满足
满足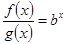 ,且
,且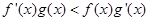 ,
, 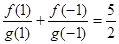 ,若
,若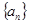 是正项等比数列,且
是正项等比数列,且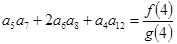 ,则
,则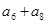 等于 .
等于 .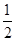 ,a4=-4,则|a1|+|a2|+…+|an|=________.
,a4=-4,则|a1|+|a2|+…+|an|=________.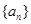 中,
中,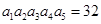 ,且
,且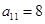 ,则
,则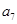 的值为( )
的值为( )