题目内容
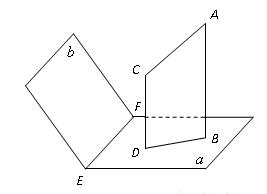
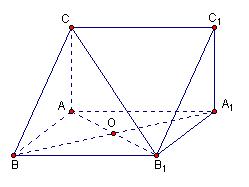
(本小题满分12分)如图,已知四棱锥
 ,底面
,底面 为菱形,
为菱形, ⊥平面
⊥平面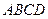 ,
,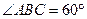 ,
,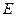 、
、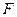 分别是
分别是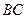 、
、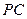 的中点。
的中点。(Ⅰ)证明:
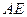 ⊥
⊥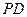 ;
;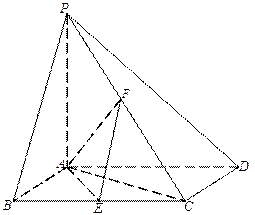 (Ⅱ)若
(Ⅱ)若 为
为 上的动点,
上的动点, 与平面
与平面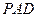 所成最大角的正切值为
所成最大角的正切值为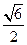 ,求二面角
,求二面角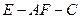 的余弦值。
的余弦值。.COM
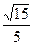
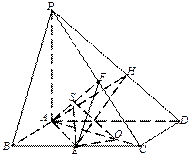 (Ⅰ)证明:由四边形
(Ⅰ)证明:由四边形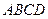 为菱形,
为菱形,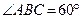 ,
,可得
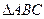 为正三角形。因为
为正三角形。因为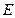 为
为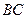 的中点,所以
的中点,所以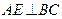 。 …………1分
。 …………1分又
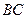 ∥
∥ ,因此
,因此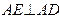 。…………………………………………………2分
。…………………………………………………2分因为
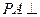 平面
平面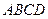 ,
,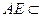 平面
平面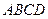 ,所以
,所以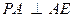 。 ………3分
。 ………3分而
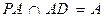 ,所以
,所以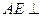 平面
平面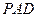 。 ………………………………4分
。 ………………………………4分又
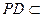 平面
平面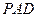 ,所以
,所以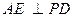 。 ……………………………………5分
。 ……………………………………5分(Ⅱ)解:设
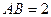 ,
, 为
为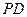 上任意一点,连接
上任意一点,连接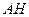 、
、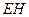
由(Ⅰ)可知:
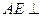 平面
平面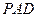 ,
,则
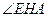 为
为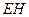 与平面
与平面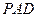 所成的角。……………………………………………6分
所成的角。……………………………………………6分在
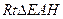 中,
中,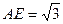 ,
,所以当
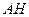 最短时,
最短时,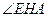 最大, ………………………………………………7分
最大, ………………………………………………7分即当
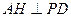 时,
时,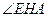 最大,此时
最大,此时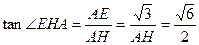 。
。 因此
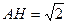 。又
。又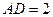 ,所以
,所以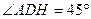 ,于是
,于是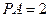 。 ……………………8分
。 ……………………8分因为
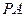 ⊥平面
⊥平面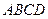 ,
,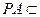 平面
平面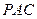 ,
,所以平面
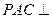 平面
平面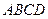 。 …………………………………………9分
。 …………………………………………9分过
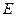 作
作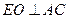 于
于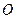 ,则由面面垂直的性质定理可知:
,则由面面垂直的性质定理可知: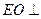 平面
平面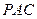 ,
,过
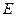 作
作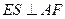 于
于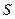 ,连接
,连接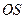 ,
,则由三垂线定理可知:
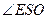 为二面角
为二面角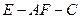 的平面角。 ……………………10分
的平面角。 ……………………10分在
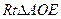 中,
中,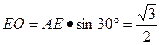 ,
,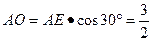
又
 是
是 的中点,在
的中点,在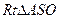 中,
中,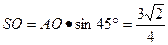
又
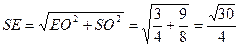 ………………………………11分
………………………………11分在
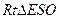 中,
中,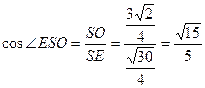
即二面角
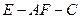 的余弦值为
的余弦值为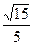 。 ………………………………12分
。 ………………………………12分
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
 平面
平面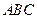 ,
,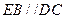 ,
,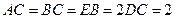 ,
,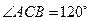 ,
,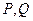 分别为
分别为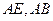 的中点.
的中点.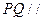 平面
平面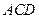 ;
;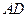 与平面
与平面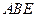 所成角的正弦值。
所成角的正弦值。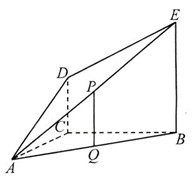
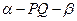 ,
,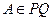 ,
,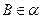 ,
,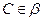 ,
,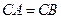 ,
,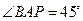 ,直线
,直线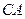 和平面
和平面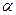 所成的角为
所成的角为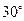 .
.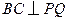 ;
;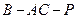 的大小.
的大小.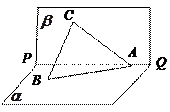
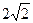 .
. (2)在线段
(2)在线段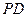 上是否存在一点
上是否存在一点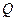 ,使
,使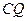 与平面
与平面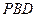 所成的角的正弦值为
所成的角的正弦值为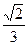 ,若存在,
,若存在, ,直线
,直线 ,给出下列命题:
,给出下列命题: ∥
∥ ; ②
; ② ∥m;
∥m; ∥
∥ ; ④
; ④ ∥
∥
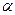 、
、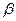 ,则
,则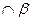 =m,n
=m,n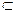
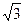 ,⊙O为其内切圆,D为BC的中点,将三角形ACD沿AD折叠,使二面角B-AD-C成直二面角,则⊙O上的圆弧扫过的曲面面积为____________.
,⊙O为其内切圆,D为BC的中点,将三角形ACD沿AD折叠,使二面角B-AD-C成直二面角,则⊙O上的圆弧扫过的曲面面积为____________.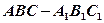 ,已知
,已知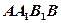 是正方形且边长为
是正方形且边长为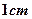 ,
,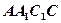 为矩形,且平面
为矩形,且平面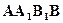
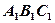 ⊥平面
⊥平面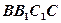 ;
;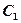 到平面
到平面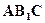 的距离。
的距离。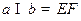 ,
,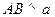 ,
,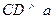 ,垂足分别为
,垂足分别为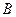 ,
,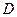 ,且
,且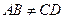 .如果增加一个条件就能推出
.如果增加一个条件就能推出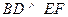 ,给出四个条件:①
,给出四个条件:①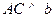 ;②
;②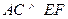 ;③
;③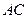 与
与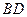 在
在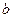 内的正投影在同一条直线上 ;④
内的正投影在同一条直线上 ;④