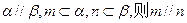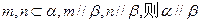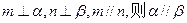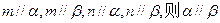题目内容
(本小题满分12分)
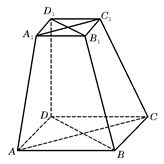
如图3,已知直二面角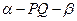 ,
,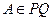 ,
,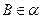 ,
,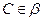 ,
,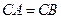 ,
,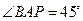 ,直线
,直线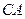 和平面
和平面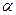 所成的角为
所成的角为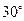 .
.
(I)证明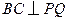 ;
;
(II)求二面角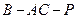 的大小.
的大小.
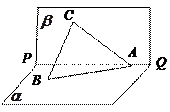
如图3,已知直二面角
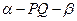 ,
,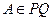 ,
,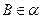 ,
,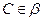 ,
,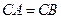 ,
,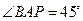 ,直线
,直线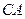 和平面
和平面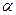 所成的角为
所成的角为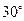 .
.(I)证明
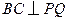 ;
;(II)求二面角
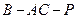 的大小.
的大小.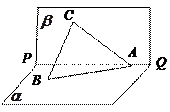
(I)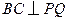
(II)二面角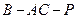 的大小为
的大小为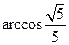
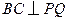
(II)二面角
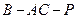 的大小为
的大小为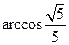
解:(I)在平面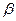 内过点
内过点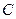 作
作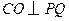 于点
于点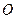 ,连结
,连结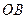 .
.
因为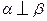 ,
,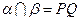 ,所以
,所以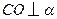 ,
,
又因为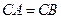 ,所以
,所以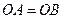 .
.
而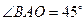 ,所以
,所以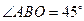 ,
,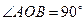 ,从而
,从而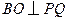 ,又
,又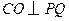 ,
,
所以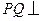 平面
平面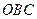 .因为
.因为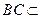 平面
平面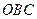 ,故
,故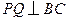 .
.
(II)解法一:由(I)知,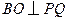 ,又
,又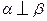 ,
,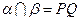 ,
,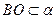 ,所以
,所以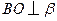 .
.
过点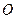 作
作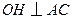 于点
于点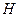 ,连结
,连结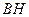 ,由三垂线定理知,
,由三垂线定理知,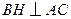 .
.
故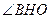 是二面角
是二面角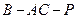 的平面角.
的平面角.
由(I)知,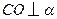 ,所以
,所以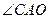 是
是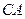 和平面
和平面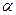 所成的角,则
所成的角,则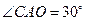 ,
,
不妨设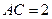 ,则
,则 ,
,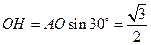 .
.
在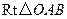 中,
中,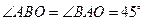 ,所以
,所以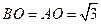 ,
,
于是在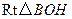 中,
中,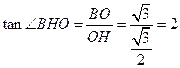 .
.
故二面角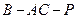 的大小为
的大小为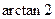 .
.
解法二:由(I)知,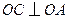 ,
,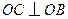 ,
,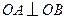 ,故可以
,故可以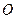 为原点,分别以直线
为原点,分别以直线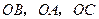 为
为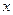 轴,
轴,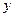 轴,
轴,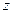 轴建立空间直角坐标系(如图).
轴建立空间直角坐标系(如图).
因为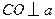 ,所以
,所以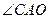 是
是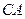 和平面
和平面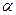 所成的角,则
所成的角,则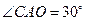 .
.
不妨设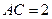 ,则
,则 ,
,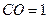 .
.
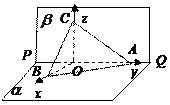 在
在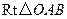 中,
中,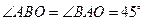 ,
,
所以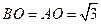 .
.
则相关各点的坐标分别是
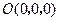 ,
,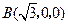 ,
,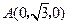 ,
,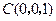 .
.
所以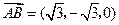 ,
,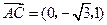 .
.
设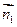
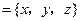 是平面
是平面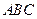 的一个法向量,由
的一个法向量,由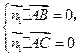 得
得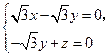
取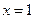 ,得
,得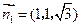 .
.
易知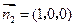 是平面
是平面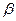 的一个法向量.
的一个法向量.
设二面角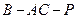 的平面角为
的平面角为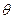 ,由图可知,
,由图可知,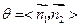 .
.
所以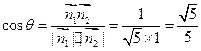 .
.
故二面角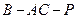 的大小为
的大小为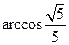 .
.
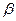 内过点
内过点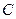 作
作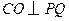 于点
于点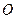 ,连结
,连结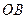 .
.因为
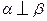 ,
,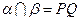 ,所以
,所以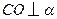 ,
,又因为
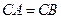 ,所以
,所以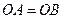 .
.而
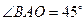 ,所以
,所以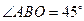 ,
,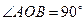 ,从而
,从而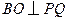 ,又
,又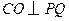 ,
,所以
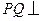 平面
平面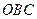 .因为
.因为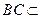 平面
平面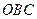 ,故
,故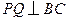 .
.(II)解法一:由(I)知,
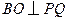 ,又
,又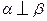 ,
,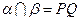 ,
,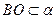 ,所以
,所以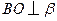 .
.过点
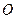 作
作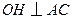 于点
于点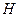 ,连结
,连结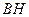 ,由三垂线定理知,
,由三垂线定理知,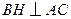 .
.故
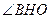 是二面角
是二面角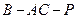 的平面角.
的平面角.由(I)知,
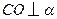 ,所以
,所以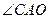 是
是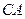 和平面
和平面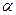 所成的角,则
所成的角,则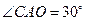 ,
,不妨设
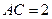 ,则
,则 ,
,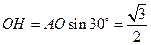 .
.在
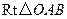 中,
中,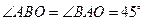 ,所以
,所以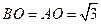 ,
,于是在
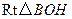 中,
中,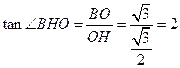 .
.故二面角
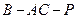 的大小为
的大小为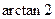 .
.解法二:由(I)知,
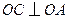 ,
,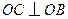 ,
,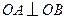 ,故可以
,故可以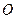 为原点,分别以直线
为原点,分别以直线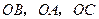 为
为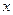 轴,
轴,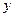 轴,
轴,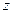 轴建立空间直角坐标系(如图).
轴建立空间直角坐标系(如图).因为
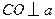 ,所以
,所以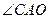 是
是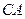 和平面
和平面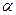 所成的角,则
所成的角,则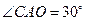 .
.不妨设
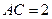 ,则
,则 ,
,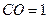 .
.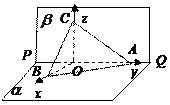 在
在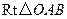 中,
中,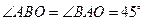 ,
,所以
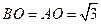 .
.则相关各点的坐标分别是
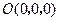 ,
,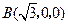 ,
,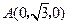 ,
,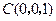 .
.所以
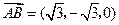 ,
,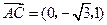 .
.设
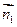
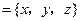 是平面
是平面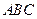 的一个法向量,由
的一个法向量,由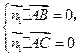 得
得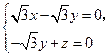
取
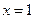 ,得
,得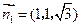 .
.易知
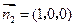 是平面
是平面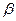 的一个法向量.
的一个法向量.设二面角
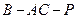 的平面角为
的平面角为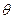 ,由图可知,
,由图可知,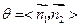 .
.所以
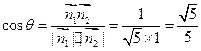 .
.故二面角
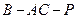 的大小为
的大小为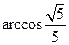 .
.
练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 中,
中,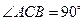 ,
,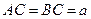 ,
, 分别为棱
分别为棱 的中点,
的中点,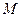 为棱
为棱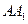 上的点,二面角
上的点,二面角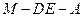 为
为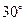 .
.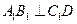 ;
; 的长,并求点
的长,并求点 到平面
到平面 的距离.
的距离.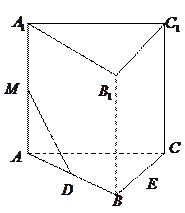
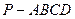 ,底面
,底面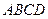 为菱形,
为菱形,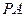 ⊥平面
⊥平面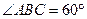 ,
,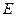 、
、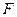 分别是
分别是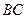 、
、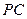 的中点。
的中点。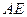 ⊥
⊥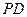 ;
;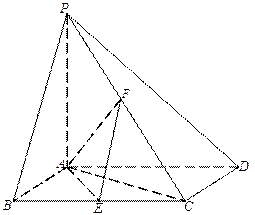 (Ⅱ)若
(Ⅱ)若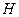 为
为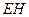 与平面
与平面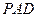 所成最大角的正切值为
所成最大角的正切值为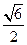 ,求二面角
,求二面角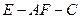 的余弦值。
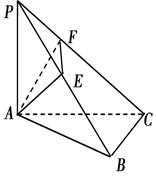
的余弦值。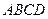 为平行四边形,
为平行四边形,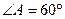 ,
,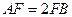 ,
,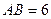 ,点
,点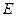 在
在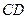 上,
上,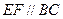 ,
,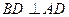 ,
,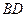 与
与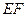 相交于
相交于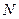 .现将四边形
.现将四边形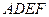 沿
沿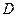 在平面
在平面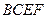 上的射影恰在直线
上的射影恰在直线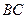 上.
上.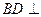 平面
平面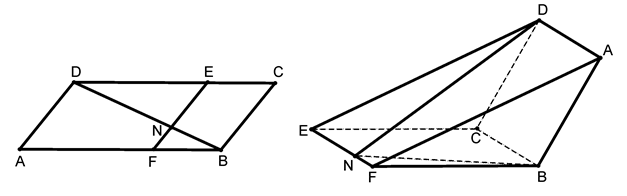
 、
、 ,两个不同的平面
,两个不同的平面 则下列命题中正确的是 ( )
则下列命题中正确的是 ( ) ,则
,则
 则
则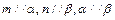 则
则
 则
则 是不同的直线,
是不同的直线, 是不重合的平面,给出下列命题:
是不重合的平面,给出下列命题: