题目内容
正三角形ABC的边长为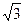 ,⊙O为其内切圆,D为BC的中点,将三角形ACD沿AD折叠,使二面角B-AD-C成直二面角,则⊙O上的圆弧扫过的曲面面积为____________.
,⊙O为其内切圆,D为BC的中点,将三角形ACD沿AD折叠,使二面角B-AD-C成直二面角,则⊙O上的圆弧扫过的曲面面积为____________.
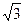 ,⊙O为其内切圆,D为BC的中点,将三角形ACD沿AD折叠,使二面角B-AD-C成直二面角,则⊙O上的圆弧扫过的曲面面积为____________.
,⊙O为其内切圆,D为BC的中点,将三角形ACD沿AD折叠,使二面角B-AD-C成直二面角,则⊙O上的圆弧扫过的曲面面积为____________.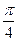 ;
;略

练习册系列答案
相关题目
题目内容
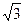 ,⊙O为其内切圆,D为BC的中点,将三角形ACD沿AD折叠,使二面角B-AD-C成直二面角,则⊙O上的圆弧扫过的曲面面积为____________.
,⊙O为其内切圆,D为BC的中点,将三角形ACD沿AD折叠,使二面角B-AD-C成直二面角,则⊙O上的圆弧扫过的曲面面积为____________.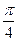 ;
;