题目内容
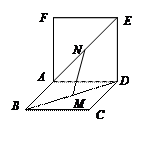
(13分)如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=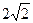 .
.
(1)求点C到平面PBD的距离;
 (2)在线段
(2)在线段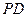 上是否存在一点
上是否存在一点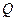 ,使
,使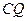 与平面
与平面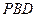 所成的角的正弦值为
所成的角的正弦值为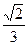 ,若存在,
,若存在,
指出点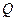 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
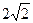 .
.(1)求点C到平面PBD的距离;
 (2)在线段
(2)在线段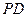 上是否存在一点
上是否存在一点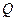 ,使
,使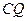 与平面
与平面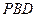 所成的角的正弦值为
所成的角的正弦值为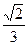 ,若存在,
,若存在,指出点
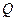 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.(1)CE=AF=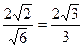
(2)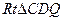 中,
中,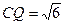 ,CD=2,DQ=
,CD=2,DQ=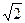 ,即Q是PD的中点。
,即Q是PD的中点。
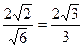
(2)
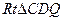 中,
中,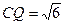 ,CD=2,DQ=
,CD=2,DQ=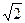 ,即Q是PD的中点。
,即Q是PD的中点。(1)∵ABCD是矩形,AD=2,BD=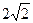 ∴AB=2
∴AB=2
∵BD⊥平面PAC,∴面PAC⊥面PBD,作CE⊥PO于E
∴CE⊥面PBD,CE=AF=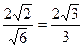 ……6分
……6分
(2)设点Q在线段PD上符合要求,∵CE⊥面PBD,
∴∠CQE是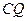 与平面
与平面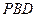 所成的角……8分
所成的角……8分
∴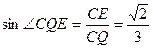 ,又CE=
,又CE=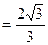 ,∴
,∴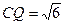 ……10分
……10分
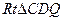 中,
中,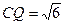 ,CD=2,∴DQ=
,CD=2,∴DQ=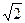 ,即Q是PD的中点。……13分
,即Q是PD的中点。……13分
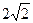 ∴AB=2
∴AB=2∵BD⊥平面PAC,∴面PAC⊥面PBD,作CE⊥PO于E
∴CE⊥面PBD,CE=AF=
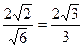 ……6分
……6分(2)设点Q在线段PD上符合要求,∵CE⊥面PBD,
∴∠CQE是
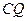 与平面
与平面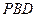 所成的角……8分
所成的角……8分∴
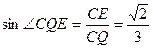 ,又CE=
,又CE=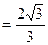 ,∴
,∴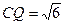 ……10分
……10分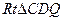 中,
中,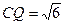 ,CD=2,∴DQ=
,CD=2,∴DQ=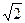 ,即Q是PD的中点。……13分
,即Q是PD的中点。……13分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
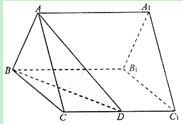
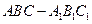 中,
中,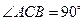 ,
,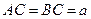 ,
,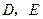 分别为棱
分别为棱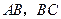 的中点,
的中点,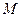 为棱
为棱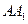 上的点,二面角
上的点,二面角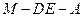 为
为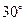 .
.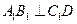 ;
;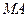 的长,并求点
的长,并求点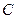 到平面
到平面 的距离.
的距离.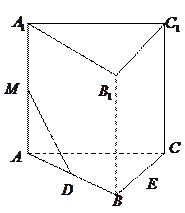
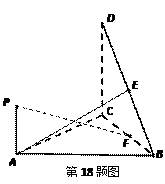
 ,
,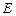 为DB的中点,
为DB的中点,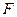 是线段
是线段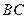 上的动点,设平面
上的动点,设平面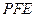 与平面
与平面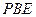 所成的平面角大小为
所成的平面角大小为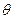 ,当
,当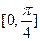 内取值时,求直线PF与平面DBC所成的角的范围。
内取值时,求直线PF与平面DBC所成的角的范围。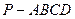 ,底面
,底面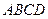 为菱形,
为菱形,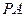 ⊥平面
⊥平面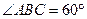 ,
,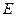 、
、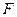 分别是
分别是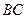 、
、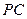 的中点。
的中点。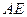 ⊥
⊥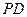 ;
;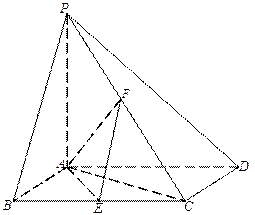 (Ⅱ)若
(Ⅱ)若 为
为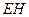 与平面
与平面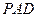 所成最大角的正切值为
所成最大角的正切值为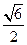 ,求二面角
,求二面角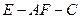 的余弦值。
的余弦值。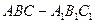 中,侧棱与底面垂直,
中,侧棱与底面垂直,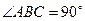 ,
,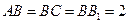 ,
, 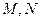 分别是
分别是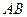 ,
,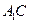 的中点.
的中点.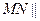 平面
平面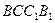 ;
; 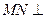 平面
平面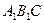 ;
;

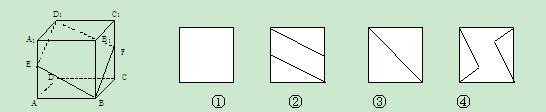
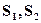 ,则
,则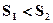
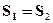
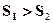
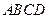 和
和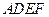 所在平面互相垂直,设
所在平面互相垂直,设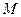 、
、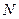 分别是
分别是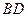 和
和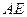 的中点,那么①
的中点,那么① 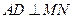 ;②
;② 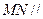 面
面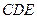 ;③
;③ 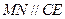 ;④
;④ 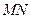 、
、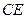 异面
异面