题目内容
11.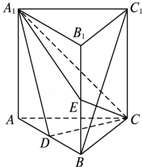 如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=2,$A{A_1}=AC=BC=\sqrt{2}$
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=2,$A{A_1}=AC=BC=\sqrt{2}$(1)证明:BC1∥平面A1CD;
(2)求异面直线BC1和A1D所成角的大小;
(3)求三棱锥A1-DEC的体积.
分析 (1)根据线面平行的判定定理,需在平面A1DE内找一条与BC1平行的直线.因为ACC1A1是矩形,故对角线互相平分,所以连结AC1,与A1C交于点O.因为D是AB的中点,连结OD,则OD是△ABC1的中位线,所以BC1∥OD,从而可证得BC1∥平面A1CD.
(2)由(1)可得∠A1DF或其补角为异面直线BC1和A1D所成角,在△A1DF中,由余弦定理可得异面直线BC1和A1D所成角的大小;
(3)先求出CD⊥平面ABB1A1,CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=1,利用体积公式求出三棱锥A1-CDE的体积.
解答 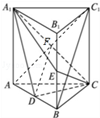 (1)证明:连接AC1与A1C相交于点F,连接DF,
(1)证明:连接AC1与A1C相交于点F,连接DF,
由矩形ACC1A1可得点F是AC1的中点,又D是AB的中点,
∴DF∥BC1,
∵BC1?平面A1CD,DF?平面A1CD,
∴BC1∥平面A1CD; …(4分)
(2)解:由(1)可得∠A1DF或其补角为异面直线BC1和A1D所成角.
DF=$\frac{1}{2}$BC1=$\frac{1}{2}\sqrt{2+2}$=1,A1D=$\sqrt{2+1}$=$\sqrt{3}$,A1F=$\frac{1}{2}$A1C=1.
在△A1DF中,由余弦定理可得:cos∠A1DF=$\frac{1+3-1}{2×1×\sqrt{3}}$=$\frac{\sqrt{3}}{2}$,
∵∠A1DF∈(0,π),∴∠A1DF=$\frac{π}{6}$,
∴异面直线BC1和A1D所成角的大小;…(8分)
(3)解:∵AC=BC,D为AB的中点,∴CD⊥AB,
∵平面ABB1A1∩平面ABC=AB,∴CD⊥平面ABB1A1,CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=1.
∴${S}_{△{A}_{1}DE}$=${S}_{矩形AB{B}_{1}{A}_{1}}$-S△BDE-${S}_{△{A}_{1}{B}_{1}E}$-${S}_{△A{A}_{1}D}$=$\frac{{3\sqrt{2}}}{4}$
∴三棱锥C-A1DE的体积V=$\frac{1}{3}×\frac{{3\sqrt{2}}}{4}×1=\frac{{\sqrt{2}}}{4}$…(12分)
点评 本题考查线面平行的证明,考查三棱锥的体积的求法,考查异面直线BC1和A1D所成角,是中档题,解题时要注意空间中线线、线面、面面间的位置关系及性质的合理运用.

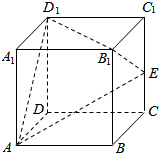 在棱长为1的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,沿A1F运动,将B1点所在的几何体削去,则剩余几何体的体积为( )
在棱长为1的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,沿A1F运动,将B1点所在的几何体削去,则剩余几何体的体积为( )| A. | $\frac{3}{4}$ | B. | $\frac{7}{8}$ | C. | $\frac{11}{12}$ | D. | $\frac{23}{24}$ |
1 2 3 4 …第一行
2 3 4 5 …第二行
3 4 5 6 …第三行
4 5 6 7 …第四行
…
第一列 第二列 第三列 第四列
根据数表中所反映的规律,第n行与第n-1列的交叉点上的数应该是( )
| A. | 2n-1 | B. | 2n+1 | C. | n2-1 | D. | 2n-2 |
| A. | 2x+y-3=0 | B. | 2x-y-1=0 | C. | x-2y-1=0 | D. | x-2y+1=0 |
 如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{1}{2}$,则下列有四个结论:
如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{1}{2}$,则下列有四个结论: