题目内容
20.设x∈R+,向量$\overrightarrow a$=(1,1),$\overrightarrow b$=(x,-2),且|$\overrightarrow a$+$\overrightarrow b$|=$\sqrt{10}$,则$\overrightarrow a$•$\overrightarrow b$=( )| A. | -2 | B. | 4 | C. | -1 | D. | 0 |
分析 通过向量的模求出x,然后利用数量积的运算法则求解即可.
解答 解:向量$\overrightarrow a$=(1,1),$\overrightarrow b$=(x,-2),且|$\overrightarrow a$+$\overrightarrow b$|=$\sqrt{10}$,
可得$\sqrt{{(x-1)}^{2}+{(-2-1)}^{2}}$=$\sqrt{10}$,
解得x=2或x=0(舍去,因为x∈R+).
则$\overrightarrow a$•$\overrightarrow b$=(1,1)•(2,-2)=2-2=0.
故选:D.
点评 本题考查向量的数量积的求法,向量的模的求法,考查计算能力.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
8.直线l经过(2,-3)和(-10,6)两点,则点(-1,1)到直线l的距离为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{7}{5}$ |
5.复数z=$\frac{-3+i}{2+i}$的共轭复数是( )
| A. | 2+i | B. | 2 i | C. | 1+i | D. | -1-i |
 如图,四棱锥P-ABCD的底面是边长为1的正方形,PD⊥底面ABCD,PD=AD,E为PC的中点,F为PB上一点,且EF⊥PB.
如图,四棱锥P-ABCD的底面是边长为1的正方形,PD⊥底面ABCD,PD=AD,E为PC的中点,F为PB上一点,且EF⊥PB.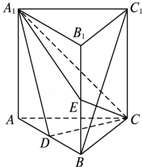 如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=2,$A{A_1}=AC=BC=\sqrt{2}$
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=2,$A{A_1}=AC=BC=\sqrt{2}$