题目内容
1.过圆x2+y2-4x+my=0上一点P(1,1)的圆的切线方程为( )| A. | 2x+y-3=0 | B. | 2x-y-1=0 | C. | x-2y-1=0 | D. | x-2y+1=0 |
分析 求出圆的方程,求出圆心与已知点确定直线方程的斜率,利用两直线垂直时斜率的乘积为-1求出过此点切线方程的斜率,即可确定出切线方程.
解答 解:∵圆x2+y2-4x+my=0上一点P(1,1),
可得1+1-4+m=0,解得m=2,圆的圆心(2,-1),过(1,1)与(2,-1)直线斜率为-2,
∴过(1,1)切线方程的斜率为$\frac{1}{2}$,
则所求切线方程为y-1=$\frac{1}{2}$(x-1),即x-2y+1=0.
故选:D.
点评 此题考查了直线与圆的位置关系,涉及的知识有:两直线垂直时斜率满足的关系,以及直线的点斜式方程,找出切线方程的斜率是解本题的关键.

练习册系列答案
相关题目
11.在△ABC中,若sinA:sinB:sinC=2:3:4,则△ABC是( )
| A. | 直角三角形 | B. | 钝角三角形 | C. | 锐三角形 | D. | 等腰直角三角形 |
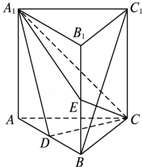 如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=2,$A{A_1}=AC=BC=\sqrt{2}$
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=2,$A{A_1}=AC=BC=\sqrt{2}$ 如图所示,圆O的直径AB=10,C为圆周上一点,BC=5,过C作圆的切线l,则点A到直线l的距离AD为$\frac{15}{2}$.
如图所示,圆O的直径AB=10,C为圆周上一点,BC=5,过C作圆的切线l,则点A到直线l的距离AD为$\frac{15}{2}$.