在△ABC中.BC=4.AC=5.AB=$\sqrt{21}$.则内角C=60°．题目和参考答案——青夏教育精英家教网—

题目内容

1．在△ABC中，BC=4，AC=5，AB=$\sqrt{21}$，则内角C=60°．

分析由题意和余弦定理求出cosC的值，再由内角的范围和特殊角的余弦值求出角C的值．

解答解：由题意知，在△ABC中，BC=4，AC=5，AB=$\sqrt{21}$，
由余弦定理得，cosC=$\frac{A{C}^{2}+B{C}^{2}-A{B}^{2}}{2AC•BC}$=$\frac{25+16-21}{2×5×4}$=$\frac{1}{2}$，
又0＜C＜180°，则C=60°，
故答案为：60°．

点评本题考查余弦定理的应用，注意内角的范围，属于基础题．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

12．已知一圆锥的底面是半径为1cm的圆，若圆锥的侧面积是底面积的3倍，则该圆锥的体积是$\frac{2\sqrt{2}π}{3}$cm³．

9．已知$f（x）=\left\{{\begin{array}{l}{{2^{x-2}}}\\{a-x}\end{array}}\right.$ $\begin{array}{l}{x＞1}\\{0≤x＜1}\end{array}$，且$f（{\frac{f（2）}{2}}）=\frac{1}{2}$，则实数a=（　　）

16．已知条件p：{x||x-a|＜3}，条件q：{x|x²-2x-3＜0}，且q是p的充分不必要条件，则a的取值范围是[0，2]．

6．复数z=1-i，则$\frac{z}{\bar z-1}$=（　　）

13．对a，b∈R，记max{a，b}=$\left\{\begin{array}{l}a{，_{\;}}a≥b\\ b{，_{\;}}a＜b\end{array}\right.$，函数f（x）=max{|x+1|，|x-m|}（x∈R）的最小值是$\frac{3}{2}$，则实数m的值是2或-4．

10．

如图，四棱锥P-ABCD的底面是边长为1的正方形，PD⊥底面ABCD，PD=AD，E为PC的中点，F为PB上一点，且EF⊥PB．
（1）证明：PA∥平面EDB；
（2）证明：PB⊥平面EFD；
（3）求三棱锥B-ADF的体积．

11．

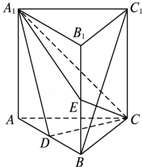如图，直三棱柱ABC-A₁B₁C₁中，D、E分别是AB、BB₁的中点，AB=2，$A{A_1}=AC=BC=\sqrt{2}$
（1）证明：BC₁∥平面A₁CD；
（2）求异面直线BC₁和A₁D所成角的大小；
（3）求三棱锥A₁-DEC的体积．

试题分类