题目内容
3.观察数表:1 2 3 4 …第一行
2 3 4 5 …第二行
3 4 5 6 …第三行
4 5 6 7 …第四行
…
第一列 第二列 第三列 第四列
根据数表中所反映的规律,第n行与第n-1列的交叉点上的数应该是( )
| A. | 2n-1 | B. | 2n+1 | C. | n2-1 | D. | 2n-2 |
分析 由给出排列规律可知,第一行第一列交叉点上的数是1,第2行第2列交叉点上的数是3,…,第n 行与第n 列交叉点上的数构成一个等差数列,先求出第n行与第n列的交叉点上的数,进而可得第n行与第n-1列的交叉点上的数.
解答 解:由给出排列规律可知,
第一行第一列交叉点上的数是1,
第2行第2列交叉点上的数是3,
…,
交叉点上的数构成一个等差数列.
第n 行与第n 列交叉点上的数是2n-1,
故第n行与第n-1列的交叉点上的数为:2n-2,
故选:D
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
14.函数 y=cos2x+2cosx的值域是( )
| A. | [-1,3] | B. | $[-\frac{3}{2},3]$ | C. | $[-\frac{3}{2},-1]$ | D. | $[\frac{3}{2},3]$ |
18.在△ABC中,a=3,b=5,c=7,那么这个三角形的最大角是( )
| A. | 135° | B. | 150° | C. | 90° | D. | 120° |
8.直线l经过(2,-3)和(-10,6)两点,则点(-1,1)到直线l的距离为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{7}{5}$ |
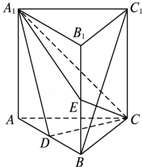 如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=2,$A{A_1}=AC=BC=\sqrt{2}$
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=2,$A{A_1}=AC=BC=\sqrt{2}$