题目内容
6.A,B,C,D是空间四点,有以下条件:①$\overrightarrow{OD}$=$\overrightarrow{OA}$+$\frac{1}{2}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$
②$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{4}$$\overrightarrow{OC}$
③$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{5}$$\overrightarrow{OC}$
④$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{6}$$\overrightarrow{OC}$
能使A,B,C,D四点一定共面的条件是④.
分析 利用空间向量共面定理即可判断出.
解答 解:对于④$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{6}$$\overrightarrow{OC}$,
∵$\frac{1}{2}+\frac{1}{3}+\frac{1}{6}$=1,由空间向量共面定理可知:能使A,B,C,D四点一定共面.
而其余的①②③不满足定理的条件.
故答案为:④
点评 本题考查了空间向量共面定理,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.函数 y=cos2x+2cosx的值域是( )
| A. | [-1,3] | B. | $[-\frac{3}{2},3]$ | C. | $[-\frac{3}{2},-1]$ | D. | $[\frac{3}{2},3]$ |
18.在△ABC中,a=3,b=5,c=7,那么这个三角形的最大角是( )
| A. | 135° | B. | 150° | C. | 90° | D. | 120° |
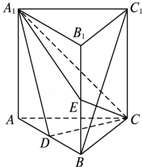 如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=2,$A{A_1}=AC=BC=\sqrt{2}$
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=2,$A{A_1}=AC=BC=\sqrt{2}$