题目内容
2．
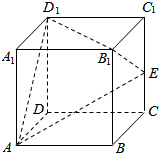在棱长为1的正方体ABCD-A1B1C1D1中，E是棱CC1的中点，F是侧面BCC1B1内（包括边）的动点，且A1F∥平面D1AE，沿A1F运动，将B1点所在的几何体削去，则剩余几何体的体积为（ ）| A． | $\frac{3}{4}$ | B． | $\frac{7}{8}$ | C． | $\frac{11}{12}$ | D． | $\frac{23}{24}$ |
分析 分别取B1B、B1C1的中点M、N，连接AM、MN、AN，证明平面A1MN∥平面D1AE，可得点F的轨迹是线段MN，即可求出剩余几何体的体积．
解答 
解：分别取B1B、B1C1的中点M、N，连接AM、MN、AN，则
∵A1M∥D1E，A1M?平面D1AE，D1E?平面D1AE，∴A1M∥平面D1AE．
同理可得MN∥平面D1AE，
∵A1M、MN是平面A1MN内的相交直线，∴平面A1MN∥平面D1AE，
由此结合A1F∥平面D1AE，可得直线A1F?平面A1MN，即点F的轨迹是线段MN，
∴${V}_{{B}_{1}-AMN}$=$\frac{1}{3}×\frac{1}{2}×1×\frac{1}{2}×\frac{1}{2}$=$\frac{1}{24}$，
∴将B1点所在的几何体削去，剩余几何体的体积为1-$\frac{1}{24}$=$\frac{23}{24}$，
故选：D．
点评 本题考查了空间直线与平面平行关系的判定与性质，考查棱锥的体积公式，综合性较强，正确的作出图形是关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，四棱锥P-ABCD的底面是边长为1的正方形，PD⊥底面ABCD，PD=AD，E为PC的中点，F为PB上一点，且EF⊥PB．
7．由函数f（x）=sin2x的图象得到g（x）=cos（2x-$\frac{π}{3}$）的图象，可将f（x）的图象（ ）
| A． | 向左平移$\frac{π}{6}$个单位 | B． | 向右平移$\frac{π}{6}$个单位 | ||
| C． | 向右平移$\frac{π}{12}$个单位 | D． | 向左平移$\frac{π}{12}$个单位 |
14．函数 y=cos2x+2cosx的值域是（ ）
| A． | [-1，3] | B． | $[-\frac{3}{2}，3]$ | C． | $[-\frac{3}{2}，-1]$ | D． | $[\frac{3}{2}，3]$ |
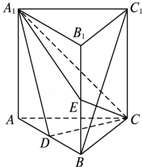如图，直三棱柱ABC-A1B1C1中，D、E分别是AB、BB1的中点，AB=2，$A{A_1}=AC=BC=\sqrt{2}$