题目内容
1.过点$(2,\frac{π}{3})$且垂直于极轴的直线的极坐标方程为ρcosθ=1.分析 将点的坐标化为直角坐标,再由直角坐标系中,求得垂线方程,再化为极坐标方程.
解答 解:点$(2,\frac{π}{3})$化为直角坐标为(2cos$\frac{π}{3}$,2sin$\frac{π}{3}$),
即为(1,$\sqrt{3}$),
则过点(1,$\sqrt{3}$)垂直于x轴的直线为x=1,
即有极坐标方程为ρcosθ=1.
故答案为:ρcosθ=1.
点评 本题考查极坐标和直角坐标的互化,同时考查与x轴垂直的直线方程,属于基础题.

练习册系列答案
相关题目
12.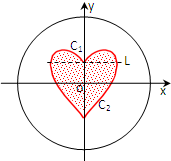 如图所示,一个圆形靶子的中心是一个“心形”图案,其中“心形”图案是由上边界C1(虚线L上方部分)与下边界C2(虚线L下方部分)围成,曲线C1是函数y=$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{4}{5}}$ 的图象,曲线C2是函数y=-$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{2}{7}}$ 的图象,圆的方程为x2+y2=8,某人向靶子射出一箭(假设此人此箭一定能射中靶子且射中靶中任何一点是等可能的),则此箭恰好命中“心形”图案的概率为( )
如图所示,一个圆形靶子的中心是一个“心形”图案,其中“心形”图案是由上边界C1(虚线L上方部分)与下边界C2(虚线L下方部分)围成,曲线C1是函数y=$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{4}{5}}$ 的图象,曲线C2是函数y=-$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{2}{7}}$ 的图象,圆的方程为x2+y2=8,某人向靶子射出一箭(假设此人此箭一定能射中靶子且射中靶中任何一点是等可能的),则此箭恰好命中“心形”图案的概率为( )
 如图所示,一个圆形靶子的中心是一个“心形”图案,其中“心形”图案是由上边界C1(虚线L上方部分)与下边界C2(虚线L下方部分)围成,曲线C1是函数y=$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{4}{5}}$ 的图象,曲线C2是函数y=-$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{2}{7}}$ 的图象,圆的方程为x2+y2=8,某人向靶子射出一箭(假设此人此箭一定能射中靶子且射中靶中任何一点是等可能的),则此箭恰好命中“心形”图案的概率为( )
如图所示,一个圆形靶子的中心是一个“心形”图案,其中“心形”图案是由上边界C1(虚线L上方部分)与下边界C2(虚线L下方部分)围成,曲线C1是函数y=$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{4}{5}}$ 的图象,曲线C2是函数y=-$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{2}{7}}$ 的图象,圆的方程为x2+y2=8,某人向靶子射出一箭(假设此人此箭一定能射中靶子且射中靶中任何一点是等可能的),则此箭恰好命中“心形”图案的概率为( )| A. | $\frac{1}{4}$-$\frac{1}{18π}$ | B. | $\frac{1}{16}$-$\frac{1}{18π}$ | C. | $\frac{1}{8}$+$\frac{1}{18π}$ | D. | $\frac{1}{8}$+$\frac{36}{35π}$ |
9.已知复数z=$\frac{2-2i}{1+i}$,则z的共轭复数的虚部等于( )
| A. | 2i | B. | -2i | C. | 2 | D. | -2 |
16.执行如图所示的程序框图,结果是( )
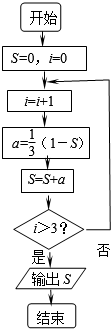

| A. | $\frac{65}{81}$ | B. | $\frac{19}{27}$ | C. | $\frac{5}{9}$ | D. | $\frac{1}{3}$ |
6.下列函数中,定义域是R且为减函数的是( )
| A. | y=ex | B. | y=-x | C. | y=lgx | D. | y=|x| |
11.已知正数组成的等比数列{an},若a1•a20=100,那么a3+a18的最小值为( )
| A. | 20 | B. | 25 | C. | 50 | D. | 不存在 |
 如图,BD是四边形ABCD的外接圆⊙O的直径,PA⊥平面ABCD,E为PD的中点,已知∠ABD=∠CBD=60°,PA=BD=2.
如图,BD是四边形ABCD的外接圆⊙O的直径,PA⊥平面ABCD,E为PD的中点,已知∠ABD=∠CBD=60°,PA=BD=2.