题目内容
9.已知复数z=$\frac{2-2i}{1+i}$,则z的共轭复数的虚部等于( )| A. | 2i | B. | -2i | C. | 2 | D. | -2 |
分析 利用复数代数形式的乘除运算化简,求得$\overline{z}$,则答案可求.
解答 解:z=$\frac{2-2i}{1+i}$=$\frac{(2-2i)(1-i)}{(1+i)(1-i)}=\frac{2(1-i)^{2}}{2}=-2i$,
∴$\overline{z}=2i$,
z的共轭复数的虚部等于2.
故选:C.
点评 本题考查复数代数形式的乘除运算,考查共轭复数的概念,是基础题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
14.已知函数f(x)=sinωx(ω>0)的图象与直线y=1的相邻交点之间的距离为π,f(x)的图象向左平移$\frac{π}{6}$个单位后,得到函数y=g(x)的图象.下列关于y=g(x)的说法正确的是( )
| A. | 图象关于点$({-\frac{π}{3},0})$中心对称 | B. | 图象关于$x=-\frac{π}{6}$轴对称 | ||
| C. | 在区间$[{-\frac{5π}{12},-\frac{π}{6}}]$上单调递增 | D. | 在区间$[{-\frac{π}{6},\frac{π}{3}}]$上单调递减 |
 已知某地区小学生3500人,初中生4500人,高中生2000人,近视情况如图所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为200,20.
已知某地区小学生3500人,初中生4500人,高中生2000人,近视情况如图所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为200,20.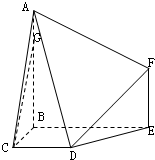 如图,在多面体ABCDEF中,BA⊥BE,BA⊥BC,BE⊥BC,AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1,G在线段AB上,且BG=3GA.
如图,在多面体ABCDEF中,BA⊥BE,BA⊥BC,BE⊥BC,AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1,G在线段AB上,且BG=3GA. 以下茎叶图记录了某赛季甲、乙两名篮球运动员参加11场比赛的得分(单位:分)若甲运动员的中位数为a,乙运动员的众数为b,则a-b的值是8.
以下茎叶图记录了某赛季甲、乙两名篮球运动员参加11场比赛的得分(单位:分)若甲运动员的中位数为a,乙运动员的众数为b,则a-b的值是8.