题目内容
11. 如图,BD是四边形ABCD的外接圆⊙O的直径,PA⊥平面ABCD,E为PD的中点,已知∠ABD=∠CBD=60°,PA=BD=2.
如图,BD是四边形ABCD的外接圆⊙O的直径,PA⊥平面ABCD,E为PD的中点,已知∠ABD=∠CBD=60°,PA=BD=2.(1)求证:CE∥平面PAB;
(2)求平面PCE与平面BCD所成锐角二面角的余弦值.
分析 (1)证明:OE∥平面PAB,OC∥平面PAB,可得平面OCE∥平面PAB,即可证明CE∥平面PAB;
(2)利用三角形的面积比,即可求平面PCE与平面BCD所成锐角二面角的余弦值.
解答 (1)证明:因为E为PD的中点,O为BD的中点,
所以OE∥PB,
因为OE?平面PAB,PB?平面PAB,
所以OE∥平面PAB
因为∠ABD=∠CBD=60°,
所以∠ABD=∠COB=60°,
所以AB∥OC,
因为OC?平面PAB,AB?平面PAB,
所以OC∥平面PAB,
因为OC∩OE=O,
所以平面OCE∥平面PAB
因为CE?平面OCE,
所以CE∥平面PAB;
(2)解:由题意,AB=1,PA=2,所以PB=$\sqrt{3}$,所以OE=$\frac{\sqrt{3}}{2}$,PC=2,PE=CE=$\frac{\sqrt{7}}{2}$,
所以${S}_{△PCE}=\frac{1}{2}×2×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,
因为S△BOC=$\frac{\sqrt{3}}{4}$,
所以平面PCE与平面BCD所成锐角二面角的余弦值为$\frac{\frac{\sqrt{3}}{4}}{\frac{\sqrt{3}}{2}}$=$\frac{1}{2}$.
点评 本题是中档题,考查棱锥中直线与平面的位置关系,二面角的求法,考查空间想象能力,计算能力,转化思想的应用.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
3.已知某几何体的三视图如图所示,则该几何体的外接球的表面积为( )
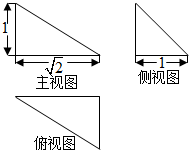

| A. | π | B. | 2π | C. | 3π | D. | 4π |
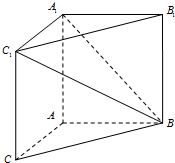 如图,在三棱柱ABC-A1B1C1中,AB=3,AA1=AC=4,AA1⊥平面ABC; AB⊥AC,
如图,在三棱柱ABC-A1B1C1中,AB=3,AA1=AC=4,AA1⊥平面ABC; AB⊥AC,


 已知某地区小学生3500人,初中生4500人,高中生2000人,近视情况如图所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为200,20.
已知某地区小学生3500人,初中生4500人,高中生2000人,近视情况如图所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为200,20.