题目内容
13.在直角坐标系xOy中,若角α的始边为x轴的非负半轴,终边为射线l:y=2$\sqrt{2}$x(x≥0).(1)求sin(2α+$\frac{π}{6}$)的值;
(2)若点P,Q分别是角α始边、终边上的动点,且PQ=4,求△POQ面积最大时,点P,Q的坐标.
分析 (1)根据角α的始边为x轴的非负半轴,终边为射线l,利用任意角的三角函数定义求出sinα与cosα的值,进而确定出sin2α与cos2α的值,原式利用两角和与差的正弦函数公式化简,将各自的值代入计算即可求出值;
(2)根据题意设出P与Q坐标,进而表示出PQ2,把PQ=4代入并利用基本不等式求出ab的最大值,确定出面积的最大值,进而求出此时P与Q的坐标即可.
解答 解:(1)由射线l的方程为y=2$\sqrt{2}$x(x≥0),可得sinα=$\frac{2\sqrt{2}}{3}$,cosα=$\frac{1}{3}$,
∴sin2α=2sinαcosα=$\frac{4\sqrt{2}}{9}$,cos2α=cos2α-sin2α=-$\frac{7}{9}$,
则sin(2α+$\frac{π}{6}$)=sin2αcos$\frac{π}{6}$+cos2αsin$\frac{π}{6}$=$\frac{2\sqrt{6}}{9}$-$\frac{7}{18}$;
(2)设P(a,0),Q(b,2$\sqrt{2}$b)(a>0,b>0),
在△POQ中,PQ=4,即PQ2=(a-b)2+8b2=16,
整理得:16=a2+9b2-2ab≥6ab-2ab=4ab,即ab≤4,
∴S△POQ=$\sqrt{2}$ab≤4$\sqrt{2}$,当且仅当a=3b,即a=2$\sqrt{3}$,b=$\frac{2\sqrt{3}}{3}$取得等号,
则△POQ面积最大时,点P,Q的坐标分别为P(2$\sqrt{3}$,0),Q($\frac{2\sqrt{3}}{3}$,$\frac{4\sqrt{6}}{3}$).
点评 此题考查了两角和与差的正弦函数公式,二倍角的正弦、余弦函数公式,以及基本不等式的运用,熟练掌握公式是解本题的关键.

| A. | π | B. | 2π | C. | 3π | D. | 4π |
| A. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] | B. | (-∞,-$\frac{\sqrt{3}}{3}$]∪[$\frac{\sqrt{3}}{3}$,+∞) | C. | $[{-\sqrt{3},\sqrt{3}}]$ | D. | $({-∞,-\sqrt{3}}]∪[{\sqrt{3},+∞})$ |
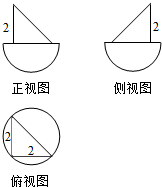 已知某几何体的三视图如图所示,其中正视图、侧视图均是由直角三角形与半圆构成,俯视图由圆与内接直角三角形构成,根据图中的数据可得此几何体体积为( )
已知某几何体的三视图如图所示,其中正视图、侧视图均是由直角三角形与半圆构成,俯视图由圆与内接直角三角形构成,根据图中的数据可得此几何体体积为( )| A. | $\frac{4\sqrt{2}π}{3}$+$\frac{4}{3}$ | B. | $\frac{8\sqrt{2}π}{3}$+$\frac{4}{3}$ | C. | $\frac{4\sqrt{2}π}{3}$+2 | D. | $\frac{8\sqrt{2}π}{3}$+2 |
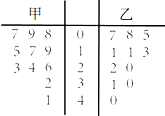 以下茎叶图记录了某赛季甲、乙两名篮球运动员参加11场比赛的得分(单位:分)若甲运动员的中位数为a,乙运动员的众数为b,则a-b的值是8.
以下茎叶图记录了某赛季甲、乙两名篮球运动员参加11场比赛的得分(单位:分)若甲运动员的中位数为a,乙运动员的众数为b,则a-b的值是8.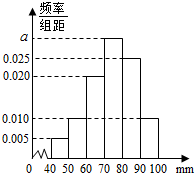 将一批工件的尺寸在(40~100mm之间)分成六段,即[40,50),[50,60),…,[90,100),得到如图的频率分布直方图,则图中实数a的值为0.03.
将一批工件的尺寸在(40~100mm之间)分成六段,即[40,50),[50,60),…,[90,100),得到如图的频率分布直方图,则图中实数a的值为0.03.