题目内容
12.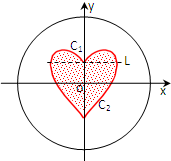 如图所示,一个圆形靶子的中心是一个“心形”图案,其中“心形”图案是由上边界C1(虚线L上方部分)与下边界C2(虚线L下方部分)围成,曲线C1是函数y=$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{4}{5}}$ 的图象,曲线C2是函数y=-$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{2}{7}}$ 的图象,圆的方程为x2+y2=8,某人向靶子射出一箭(假设此人此箭一定能射中靶子且射中靶中任何一点是等可能的),则此箭恰好命中“心形”图案的概率为( )
如图所示,一个圆形靶子的中心是一个“心形”图案,其中“心形”图案是由上边界C1(虚线L上方部分)与下边界C2(虚线L下方部分)围成,曲线C1是函数y=$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{4}{5}}$ 的图象,曲线C2是函数y=-$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{2}{7}}$ 的图象,圆的方程为x2+y2=8,某人向靶子射出一箭(假设此人此箭一定能射中靶子且射中靶中任何一点是等可能的),则此箭恰好命中“心形”图案的概率为( )| A. | $\frac{1}{4}$-$\frac{1}{18π}$ | B. | $\frac{1}{16}$-$\frac{1}{18π}$ | C. | $\frac{1}{8}$+$\frac{1}{18π}$ | D. | $\frac{1}{8}$+$\frac{36}{35π}$ |
分析 根据图象的对称性求出当x>0时的面积,利用积分的意义,求出对应区域的面积进行求解即可.
解答 解:由y=$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{4}{5}}$=-$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{2}{7}}$ 得x=1,
当x>0时,y轴由此的面积S=${∫}_{0}^{1}$[$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{4}{5}}$-(-$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{2}{7}}$ )]dx
=${∫}_{0}^{1}$(2$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{4}{5}}$-x${\;}^{\frac{2}{7}}$ )dx=2${∫}_{0}^{1}$$\sqrt{1-{x}^{2}}$dx+${∫}_{0}^{1}$(x${\;}^{\frac{4}{5}}$-x${\;}^{\frac{2}{7}}$ )dx,
${∫}_{0}^{1}$$\sqrt{1-{x}^{2}}$dx的几何意义为$\frac{1}{4}$单位圆的面积,为$\frac{π}{4}$,
${∫}_{0}^{1}$(x${\;}^{\frac{4}{5}}$-x${\;}^{\frac{2}{7}}$ )dx=($\frac{5}{9}$x${\;}^{\frac{9}{5}}$-$\frac{7}{9}$x${\;}^{\frac{9}{7}}$)|${\;}_{0}^{1}$=$\frac{5}{9}$-$\frac{7}{9}$=-$\frac{2}{9}$,
则S=$\frac{π}{4}$-$\frac{2}{9}$,
故阴影部分的面积为S=2($\frac{π}{4}$-$\frac{2}{9}$)=$\frac{π}{2}-\frac{4}{9}$,
大圆的面积S=π×8=8π,
故此箭恰好命中“心形”图案的概率P=$\frac{\frac{π}{2}-\frac{4}{9}}{8π}$=$\frac{1}{16}$-$\frac{1}{18π}$,
故选:B
点评 本题主要考查几何概型的概率的计算,根据条件结合积分的几何意义求出对应区域的面积是解决本题的关键.综合性较强.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案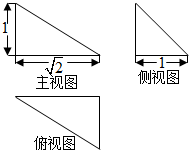
| A. | π | B. | 2π | C. | 3π | D. | 4π |
 已知某地区小学生3500人,初中生4500人,高中生2000人,近视情况如图所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为200,20.
已知某地区小学生3500人,初中生4500人,高中生2000人,近视情况如图所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为200,20.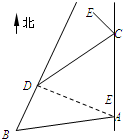 如图,甲船从A处以每小时30海里的速度沿正北方向航行,乙船在B处沿固定方向匀速航行,B在A北偏西105°方向用与B相距10$\sqrt{2}$ 海里处.当甲船航行20分钟到达C处时,乙船航行到甲船的北偏西120°方向的D处,此时两船相距10海里.
如图,甲船从A处以每小时30海里的速度沿正北方向航行,乙船在B处沿固定方向匀速航行,B在A北偏西105°方向用与B相距10$\sqrt{2}$ 海里处.当甲船航行20分钟到达C处时,乙船航行到甲船的北偏西120°方向的D处,此时两船相距10海里.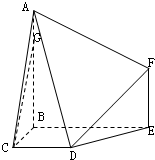 如图,在多面体ABCDEF中,BA⊥BE,BA⊥BC,BE⊥BC,AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1,G在线段AB上,且BG=3GA.
如图,在多面体ABCDEF中,BA⊥BE,BA⊥BC,BE⊥BC,AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1,G在线段AB上,且BG=3GA. 以下茎叶图记录了某赛季甲、乙两名篮球运动员参加11场比赛的得分(单位:分)若甲运动员的中位数为a,乙运动员的众数为b,则a-b的值是8.
以下茎叶图记录了某赛季甲、乙两名篮球运动员参加11场比赛的得分(单位:分)若甲运动员的中位数为a,乙运动员的众数为b,则a-b的值是8.