题目内容
某商品现在售价为每件60元,每星期可卖出300件,市场反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元
(1)用定价x表示利润f(x)的函数关系;
(2)如何定价才能使利润最大?
(1)用定价x表示利润f(x)的函数关系;
(2)如何定价才能使利润最大?
考点:简单线性规划的应用
专题:计算题,函数的性质及应用
分析:(1)由题意,利用分段函数写出f(x)=
x∈N,再化简;
(2)分段求出最大值,再求最大值.
|
(2)分段求出最大值,再求最大值.
解答:
解:(1)由题意,
f(x)=
x∈N;
即f(x)=
x∈N;
(2)由(1)知,
当60≤x<90时,
f(x)对称轴为x=-
=65,
fmax(x)=f(65)=6250;
当40<x<60时,
f(x)对称轴为x=-
=57.5;
fmax(x)=f(57)=f(58)=6120;
故当定价为65元时有最大利润为6250元.
f(x)=
|
即f(x)=
|
(2)由(1)知,
当60≤x<90时,
f(x)对称轴为x=-
| 1300 |
| -20 |
fmax(x)=f(65)=6250;
当40<x<60时,
f(x)对称轴为x=-
| 2300 |
| -40 |
fmax(x)=f(57)=f(58)=6120;
故当定价为65元时有最大利润为6250元.
点评:本题考查了实际问题转化为数学问题,同时考查了分段函数的应用,属于中档题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
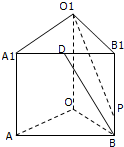 已知在直三棱柱ABO-A1B1O1中,OO1=4,OA=4,OB=3,∠AOB=90°,点D是线段A1B1的中点,点P是侧棱BB1上一点,若O1P与平面AOB所成的角正切值为
已知在直三棱柱ABO-A1B1O1中,OO1=4,OA=4,OB=3,∠AOB=90°,点D是线段A1B1的中点,点P是侧棱BB1上一点,若O1P与平面AOB所成的角正切值为