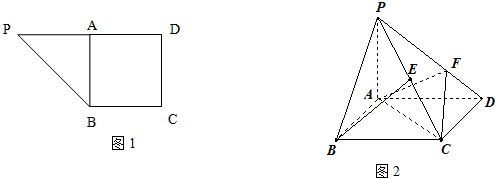
题目内容
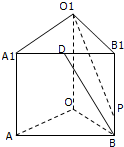已知在直三棱柱ABO-A1B1O1中，OO1=4，OA=4，OB=3，∠AOB=90°，点D是线段A1B1的中点，点P是侧棱BB1上一点，若O1P与平面AOB所成的角正切值为| 3 |
| 8 |
（1）求证：OP⊥BD；
（2）求二面角D-OP-B的余弦值．
考点：二面角的平面角及求法,空间中直线与直线之间的位置关系
专题：空间位置关系与距离,空间角
分析：（1）以O为原点，OA为x轴，OB为y轴，OO1为z轴，建立空间直角坐标系，利用向量法能证明OP⊥BD．
（2）由题意知平面OPB的法向量
=（1，0，0），求出平面DOP的法向量，由此能求出二面角D-OP-B的余弦值．
（2）由题意知平面OPB的法向量
| n |
解答：
（1）证明：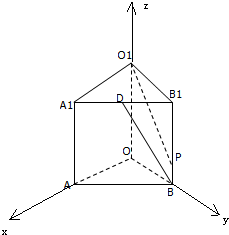
以O为原点，OA为x轴，OB为y轴，OO1为z轴，
建立空间直角坐标系，
O1P与平面AOB所成的角正切值为
，
∴
与平面AOB的法向量
=（0，0，1）的余弦值为
，
设P（0，3，t），O1（0，0，4），
∴
=（0，3，t-4），
∴|cos＜
，
＞|=|
|=
，解得t=
．
∴
=（0，3，
），
A1（4，0，4），B1（0，3，4），
D（2，
，4），B（0，3，0），
=（2，-
，4），
∴
•
=0，
∴OP⊥BD．
（2）解：由题意知平面OPB的法向量
=（1，0，0），
设平面DOP的法向量
=（x，y，z），
∵
=(2，
，4)，
=（0，3，
），
∴
，
取z=8，得
=（-
，-3，8），
∴|cos＜
，
＞|=|
|=
．
∴二面角D-OP-B的余弦值为
．
以O为原点，OA为x轴，OB为y轴，OO1为z轴，建立空间直角坐标系，
O1P与平面AOB所成的角正切值为
| 3 |
| 8 |
∴
| O1P |
| n |
3
| ||
| 73 |
设P（0，3，t），O1（0，0，4），
∴
| O1P |
∴|cos＜
| O1P |
| n |
| t-4 | ||
|
8
| ||
| 73 |
| 9 |
| 8 |
∴
| OP |
| 9 |
| 8 |
A1（4，0，4），B1（0，3，4），
D（2，
| 3 |
| 2 |
| BD |
| 3 |
| 2 |
∴
| BD |
| OP |
∴OP⊥BD．
（2）解：由题意知平面OPB的法向量
| n |
设平面DOP的法向量
| m |
∵
| OD |
| 3 |
| 2 |
| OP |
| 9 |
| 8 |
∴
|
取z=8，得
| m |
| 55 |
| 4 |
∴|cos＜
| m |
| n |
-
| ||||
|
55
| ||
| 4177 |
∴二面角D-OP-B的余弦值为
55
| ||
| 4177 |
点评：本题考查异面直线垂直的证明，考查二面角的余弦值的求法，是中档题，解题时要认真审题，注意向量法的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
