题目内容
求函数y=cos（2x+
）图象的一个对称中心．
| π |
| 3 |
考点：余弦函数的图象
专题：三角函数的图像与性质
分析：对于函数y=cos（2x+
），令2x+
=kπ+
，k∈z，求得x的值，可得函数的图象的对称中心．
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
解答：
解：对于函数y=cos（2x+
），令2x+
=kπ+
，k∈z，可得x=
+
，
故函数的图象的对称中心为（
+
，0），k∈z，
故函数y=cos（2x+
）图象的一个对称中心为（
，0）．
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 12 |
故函数的图象的对称中心为（
| kπ |
| 2 |
| π |
| 12 |
故函数y=cos（2x+
| π |
| 3 |
| π |
| 12 |
点评：本题主要考查余弦函数的图象的对称性，属于基础题．
练习册系列答案
相关题目
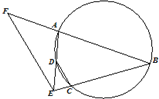如图，A，B，C，D四点在同一圆上，BC与AD的延长线交于点E，点F在BA的延长线上，若
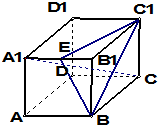在正方体ABCD-A1B1C1D1中，点E是棱A1B1的中点，