题目内容
已知函数f(x)=xlnx-x.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求函数f(x)的极值.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求函数f(x)的极值.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)f′(x)=lnx+1-1=lnx,可得f′(1)=0,即为切线的斜率,利用点斜式即可得出切线的方程;
(2)由(1)可得f′(x)=lnx,令f′(x)=lnx=0,解得x=1;分别解出f′(x)>0,f′(x)<0,即可判断出单调性,极值.
(2)由(1)可得f′(x)=lnx,令f′(x)=lnx=0,解得x=1;分别解出f′(x)>0,f′(x)<0,即可判断出单调性,极值.
解答:
解:(1)f′(x)=lnx+1-1=lnx,
∴f′(1)=0,
又f(1)=-1,
∴曲线y=f(x)在点(1,f(1))处的切线方程为y=-1.
(2)由(1)可得f′(x)=lnx,
令f′(x)=lnx=0,解得x=1;
当x>1时,f′(x)>0,函数f(x)单调递增;当0<x<1时,f′(x)<0,函数f(x)单调递减法.
∴当x=1时,函数f(x)取得极小值,f(1)=-1.
∴f′(1)=0,
又f(1)=-1,
∴曲线y=f(x)在点(1,f(1))处的切线方程为y=-1.
(2)由(1)可得f′(x)=lnx,
令f′(x)=lnx=0,解得x=1;
当x>1时,f′(x)>0,函数f(x)单调递增;当0<x<1时,f′(x)<0,函数f(x)单调递减法.
∴当x=1时,函数f(x)取得极小值,f(1)=-1.
点评:本题考查了利用导数研究函数的单调性极值、几何意义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
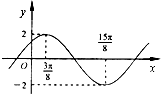 已知函数f(x)=2sin(ωx+ϕ)(ω>0,0<ϕ<π)的图象如图所示,则ω等于( )
已知函数f(x)=2sin(ωx+ϕ)(ω>0,0<ϕ<π)的图象如图所示,则ω等于( )A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
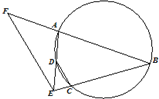 如图,A,B,C,D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上,若
如图,A,B,C,D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上,若 已知等差数列{an}的公差为d,前n项和为Sn,且满足
已知等差数列{an}的公差为d,前n项和为Sn,且满足