题目内容
设函数f(x)=-x(x-a)2(x∈R),其中a∈R.
(1)当a=1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)当a≠0时,求函数f(x)的极大值和极小值;
(3)当a=3时,函数图象与直线y=m有三个交点,求实数m的取值范围.
(1)当a=1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)当a≠0时,求函数f(x)的极大值和极小值;
(3)当a=3时,函数图象与直线y=m有三个交点,求实数m的取值范围.
考点:利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用,导数的综合应用
分析:(1)当a=1时,f(x)=-x(x-1)2=-x3+2x2-x,f′(x)=-3x2+4x-1,代入x=2,从而求切线方程;
(2)f(x)=-x(x-a)2=-x3+2ax2-a2x,f′(x)=-3x2+4ax-a2=-(3x-a)(x-a);讨论a,从而确定极值点与极值;
(3)结合函数的图象及极值求实数m的取值范围.
(2)f(x)=-x(x-a)2=-x3+2ax2-a2x,f′(x)=-3x2+4ax-a2=-(3x-a)(x-a);讨论a,从而确定极值点与极值;
(3)结合函数的图象及极值求实数m的取值范围.
解答:
解:(1)当a=1时,
f(x)=-x(x-1)2=-x3+2x2-x,
f′(x)=-3x2+4x-1,
则f(2)=-8+8-2=-2,f′(2)=-12+8-1=-5;
则曲线y=f(x)在点(2,f(2))处的切线方程为
y+2=-5(x-2),
即5x+y-8=0;
(2)f(x)=-x(x-a)2=-x3+2ax2-a2x,
f′(x)=-3x2+4ax-a2=-(3x-a)(x-a);
①若a>0,
则在x=
附近,左侧f′(x)<0,右侧f′(x)>0;
故f(x)在x=
时取得极小值f(
)=-
a3;
在x=a附近,左侧f′(x)>0,右侧f′(x)<0;
故f(x)在x=a时取得极大值f(a)=0;
②若a<0,
则在x=
附近,左侧f′(x)>0,右侧f′(x)<0;
故f(x)在x=
时取得极大值f(
)=-
a3;
在x=a附近,左侧f′(x)<0,右侧f′(x)>0;
故f(x)在x=a时取得极小值f(a)=0;
(3)由(2)可知,
f(x)在(-∞,1)递减,(1.3)递增,(3,+∞)递减.
f(x)极小值=f(1)=-4;f(x)极大值=f(3)=0;
故-4<m<0.
f(x)=-x(x-1)2=-x3+2x2-x,
f′(x)=-3x2+4x-1,
则f(2)=-8+8-2=-2,f′(2)=-12+8-1=-5;
则曲线y=f(x)在点(2,f(2))处的切线方程为
y+2=-5(x-2),
即5x+y-8=0;
(2)f(x)=-x(x-a)2=-x3+2ax2-a2x,
f′(x)=-3x2+4ax-a2=-(3x-a)(x-a);
①若a>0,
则在x=
| a |
| 3 |
故f(x)在x=
| a |
| 3 |
| a |
| 3 |
| 4 |
| 27 |
在x=a附近,左侧f′(x)>0,右侧f′(x)<0;
故f(x)在x=a时取得极大值f(a)=0;
②若a<0,
则在x=
| a |
| 3 |
故f(x)在x=
| a |
| 3 |
| a |
| 3 |
| 4 |
| 27 |
在x=a附近,左侧f′(x)<0,右侧f′(x)>0;
故f(x)在x=a时取得极小值f(a)=0;
(3)由(2)可知,
f(x)在(-∞,1)递减,(1.3)递增,(3,+∞)递减.
f(x)极小值=f(1)=-4;f(x)极大值=f(3)=0;
故-4<m<0.
点评:本题考查了导数的几何意义及导数的综合应用,同时考查了数形结合的数学思想,属于难题.

练习册系列答案
相关题目
若数列{an}的通项公式为an=
,其前n项和为
,则n为( )
| 1 |
| n2+3n+2 |
| 7 |
| 18 |
| A、5 | B、6 | C、7 | D、8 |
用数字1,2,3,4,5组成无重复数字的五位数,要求1不在首位,3不在百位的五位数共有( )
| A、72 | B、78 | C、96 | D、54 |
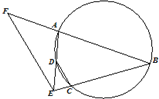 如图,A,B,C,D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上,若
如图,A,B,C,D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上,若