题目内容
已知偶函数f(x)满足f(x+1)=f(x-1),且当x∈[0,1]时,f(x)=x2,则关于x的方程f(x)=2-2|x|
在[-5,5]上根的个数是( )
在[-5,5]上根的个数是( )
| A、4个 | B、6个 | C、8个 | D、10个 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:首先,根据f(x+1)=f(x-1),得到函数f(x)的周期为2,然后,在同一坐标系中画出在[-5,5]上,函数y=f(x)和y=)=2-2|x|简图,根据图象,容易得到结果.
解答:
解:∵f(x+1)=f(x-1),
∴f(x+2)=f(x),
∴函数f(x)的周期为2,
在[-5,5]上,函数y=f(x)和y=)=2-2|x|的简图: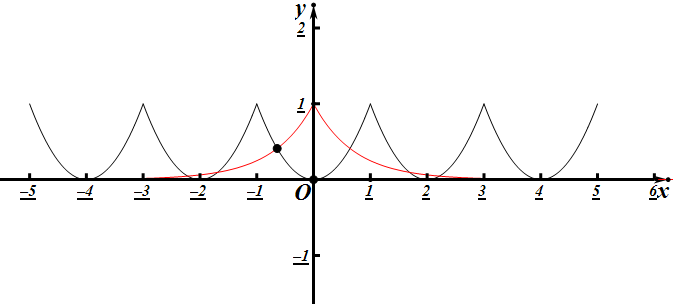
根据图象,知关于x的方程f(x)=)=2-2|x|
在[-5,5]上根的个数是10.
故选D.
∴f(x+2)=f(x),
∴函数f(x)的周期为2,
在[-5,5]上,函数y=f(x)和y=)=2-2|x|的简图:

根据图象,知关于x的方程f(x)=)=2-2|x|
在[-5,5]上根的个数是10.
故选D.
点评:本题重点考查了偶函数的性质、周期函数的概念、函数的基本性质图象等知识,属于中档题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
用数字1,2,3,4,5组成无重复数字的五位数,要求1不在首位,3不在百位的五位数共有( )
| A、72 | B、78 | C、96 | D、54 |
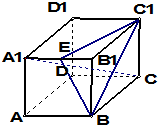 在正方体ABCD-A1B1C1D1中,点E是棱A1B1的中点,
在正方体ABCD-A1B1C1D1中,点E是棱A1B1的中点,