题目内容
在数列{an}中,a1=1,a1=1,an+1=(1+
)an+
(Ⅰ)设bn=
,求数列{bn}的通项公式;
(Ⅱ)求数列{an}的前n项和Sn;
(Ⅲ)设cn=(2n-an)2n,求证:
+
+…+
<
.
| 1 |
| n |
| n+1 |
| 2n |
(Ⅰ)设bn=
| an |
| n |
(Ⅱ)求数列{an}的前n项和Sn;
(Ⅲ)设cn=(2n-an)2n,求证:
| 1 |
| c1c2 |
| 1 |
| c2c3 |
| 1 |
| cncn+1 |
| 1 |
| 4 |
考点:数列的求和,数列的应用,数列与不等式的综合
专题:等差数列与等比数列
分析:(I)由an+1=(1+
)an+
,变形为
=
+
,即bn+1-bn=
,利用累差迭加得bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1,再利用等比数列的前n项和公式即可得出.
(II)由(I)知an=n(2-
)=2n-
,可得Sn=
-Tn,其中Tn=
+
+
+…+
+
,利用“错位相减法”即可得出.
(III) 由(II)得cn=(2n-an)2n=2n.可得
=
=
(
-
),利用“裂项求和”即可得出.
| 1 |
| n |
| n+1 |
| 2n |
| an+1 |
| n+1 |
| an |
| n |
| 1 |
| 2n |
| 1 |
| 2n |
(II)由(I)知an=n(2-
| 1 |
| 2n-1 |
| n |
| 2n-1 |
| n(2+2n) |
| 2 |
| 1 |
| 1 |
| 2 |
| 2 |
| 3 |
| 22 |
| n-1 |
| 2n-2 |
| n |
| 2n-1 |
(III) 由(II)得cn=(2n-an)2n=2n.可得
| 1 |
| cncn+1 |
| 1 |
| 4n(n+1) |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
解答:
解:(I)由an+1=(1+
)an+
,
可得
=
+
,
∴bn+1-bn=
,
利用累差迭加得bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1
=
+
+…+
+1
=
=2-
,
当n=1时,也成立.
∴数列{bn}的通项公式:bn=2-
.
(II)由(I)知an=n(2-
)=2n-
,
∴Sn=
-Tn,
其中Tn=
+
+
+…+
+
,
∴2Tn=2+2+
+…+
,
∴Tn=2+1+
+
+…+
-
=
-
=4-
,
∴Sn=n(n+1)+
-4.
(III)证明:由(II)得cn=(2n-an)2n=2n.
∴
=
=
(
-
),
∴
+
+…+
=
[(1-
)+(
-
)+…+(
-
)]
=
(1-
)<
.
| 1 |
| n |
| n+1 |
| 2n |
可得
| an+1 |
| n+1 |
| an |
| n |
| 1 |
| 2n |
∴bn+1-bn=
| 1 |
| 2n |
利用累差迭加得bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1
=
| 1 |
| 2n-1 |
| 1 |
| 2n-2 |
| 1 |
| 2 |
=
1-
| ||
1-
|
| 1 |
| 2n-1 |
当n=1时,也成立.
∴数列{bn}的通项公式:bn=2-
| 1 |
| 2n-1 |
(II)由(I)知an=n(2-
| 1 |
| 2n-1 |
| n |
| 2n-1 |
∴Sn=
| n(2+2n) |
| 2 |
其中Tn=
| 1 |
| 1 |
| 2 |
| 2 |
| 3 |
| 22 |
| n-1 |
| 2n-2 |
| n |
| 2n-1 |
∴2Tn=2+2+
| 3 |
| 2 |
| n |
| 2n-2 |
∴Tn=2+1+
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-2 |
| n |
| 2n-1 |
2(1-
| ||
1-
|
| n |
| 2n-1 |
| n+2 |
| 2n-1 |
∴Sn=n(n+1)+
| n+2 |
| 2n-1 |
(III)证明:由(II)得cn=(2n-an)2n=2n.
∴
| 1 |
| cncn+1 |
| 1 |
| 4n(n+1) |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
∴
| 1 |
| c1c2 |
| 1 |
| c2c3 |
| 1 |
| cncn+1 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| 4 |
点评:本题考查了等差数列与等比数列的通项公式及其前n项和公式,考查了数列求和方法“累加求和”、“错位相减法”、“裂项求和”,考查了推理能力与计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若数列{an}的通项公式为an=
,其前n项和为
,则n为( )
| 1 |
| n2+3n+2 |
| 7 |
| 18 |
| A、5 | B、6 | C、7 | D、8 |
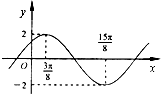 已知函数f(x)=2sin(ωx+ϕ)(ω>0,0<ϕ<π)的图象如图所示,则ω等于( )
已知函数f(x)=2sin(ωx+ϕ)(ω>0,0<ϕ<π)的图象如图所示,则ω等于( )A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
某商场对某种商品搞一次降价促销活动,现有四种降价方案.方案Ⅰ:先降价x%,后降价y%;方案Ⅱ:先降价y%,后降价x%;方案Ⅲ:先降价
%,后降价
%;方案Ⅳ:一次性降价(x+y)%(其中0<x,y<50).在上述四种方案中,降价最少的是( )
| x+y |
| 2 |
| x+y |
| 2 |
| A、方案Ⅰ | B、方案Ⅱ |
| C、方案Ⅲ | D、方案Ⅳ |
用数字1,2,3,4,5组成无重复数字的五位数,要求1不在首位,3不在百位的五位数共有( )
| A、72 | B、78 | C、96 | D、54 |
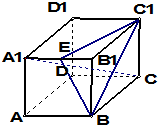 在正方体ABCD-A1B1C1D1中,点E是棱A1B1的中点,
在正方体ABCD-A1B1C1D1中,点E是棱A1B1的中点,