题目内容
16．在复平面内，复数z=$\frac{3+4i}{1-i}$对应的点在（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 利用复数的乘除运算法则化简复数，求出复数的对应点的坐标，判断即可．
解答 解：∵$z=\frac{3+4i}{1-i}=\frac{（3+4i）（1+i）}{（1-i）（1+i）}=\frac{-1+7i}{2}$，复数对应点为：$（-\frac{1}{2}，\frac{7}{2}）$．
点$（-\frac{1}{2}，\frac{7}{2}）$在第二象限，
故选B．
点评 本题考查复数的几何意义，复数乘除运算法则的应用，考查计算能力．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
7．某赛事组委会要为获奖者定做某工艺品作为奖品，其中一等奖奖品3件，二等奖奖品6件．制作一等奖和二等奖奖品所用原料完全相同，但工艺不同，故价格有所差异．现有甲、乙两家工厂可以制作奖品（一等奖、二等奖奖品均符合要求），甲厂收费便宜，但原料有限，最多只能制作4件奖品，乙厂原料充足，但收费交贵，其具体收费情况如表：
求组委会定做该工艺品至少需要花费多少元钱．
| 奖品 收费（元/件） 工厂 | 一等奖奖品 | 二等奖奖品 |
| 甲 | 500 | 400 |
| 乙 | 800 | 600 |
4．
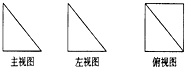如图，是一个空间几何体的主视图（正视图）、左视图、俯视图，如果图中直角三角形的直角边长均为1，那么这个几何体的侧面积为（ ）
如图，是一个空间几何体的主视图（正视图）、左视图、俯视图，如果图中直角三角形的直角边长均为1，那么这个几何体的侧面积为（ ）| A． | 1+$\sqrt{2}$ | B． | 2+$\sqrt{2}$ | C． | 1+2$\sqrt{2}$ | D． | 2+2$\sqrt{2}$ |
5．集合A={x|x2-2x≤0}，B={x|y=lg（1-x）}，则A∩（∁RB）等于（ ）
| A． | {x|0＜x≤1} | B． | {x|0≤x＜1} | C． | {x|1＜x≤2} | D． | {x|1≤x≤2} |
6．执行如图所示的程序框图，输出的x值为（ ）
| A． | 7 | B． | 6 | C． | 5 | D． | 4 |