题目内容
4.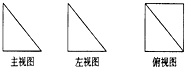 如图,是一个空间几何体的主视图(正视图)、左视图、俯视图,如果图中直角三角形的直角边长均为1,那么这个几何体的侧面积为( )
如图,是一个空间几何体的主视图(正视图)、左视图、俯视图,如果图中直角三角形的直角边长均为1,那么这个几何体的侧面积为( )| A. | 1+$\sqrt{2}$ | B. | 2+$\sqrt{2}$ | C. | 1+2$\sqrt{2}$ | D. | 2+2$\sqrt{2}$ |
分析 由已知中的三视图,可知该几何体是以俯视图为底面的四棱锥,分别求出各个侧面的面积,相加可得答案.
解答 解:解:由已知中的三视图,可知该几何体是以俯视图为底面的四棱锥,
其直观图如下图所示:
其中侧面△ABC与△ABE是腰长为1的等腰直角三角形,
其面积均为$\frac{1}{2}$,
侧面△ACD与△ADE三边长为1,$\sqrt{2}$,$\sqrt{3}$,
其面积均为$\frac{\sqrt{2}}{2}$,
故几何体的侧面积为:1+$\sqrt{2}$,
故选:A
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.设X~N(-2,$\frac{1}{4}$),则X落在(-∞,-3.5]∪[-0.5,+∞)内的概率是( )
| A. | 95.4% | B. | 99.7% | C. | 4.6% | D. | 0.3% |
12.已知F是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A、B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围为( )
| A. | (1,2) | B. | (2,1+$\sqrt{2}$) | C. | ($\frac{1}{2}$,1) | D. | (1+$\sqrt{2}$,+∞) |
16.在复平面内,复数z=$\frac{3+4i}{1-i}$对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.已知集合A={0,1,3},B={x|y=ln(x-1)},则A∩B=( )
| A. | ∅ | B. | {3} | C. | {1,3} | D. | {0,1,3} |