题目内容
11.由曲线y=$\frac{3}{x}$,x+y=4围成的平面图形绕x轴旋转而成的旋转体的体积为$\frac{8π}{3}$.分析 根据题意,这旋转一周所得旋转体的体积应该用定积分来求.此几何体的体积可以看作是$π{[∫}_{1}^{3}(4-x)^{2}dx-{∫}_{1}^{3}\frac{9}{{x}^{2}}dx]$,求出这个定积分的值,即求得题中的体积.
解答 解:曲线y=$\frac{3}{x}$与x+y=4交于(1,3)点和(3,1)点,
由曲线y=$\frac{3}{x}$,x+y=4围成的平面图形绕x轴旋转而成的旋转体的体积V=$π{[∫}_{1}^{3}(4-x)^{2}dx-{∫}_{1}^{3}\frac{9}{{x}^{2}}dx]$=$\frac{8π}{3}$,
故答案为:$\frac{8π}{3}$
点评 本题考查用定积分求简单几何体的体积,求解的关键是找出被积函数来及积分区间.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知全集U=R,集合A={x|x2>2x+3},B={x|log3x>1},则下列关系正确的是( )
| A. | A∪∁UB=R | B. | B∪∁UA=R | C. | A∪B=R | D. | A∩B=A |
6.定义:$|\begin{array}{l}{{a}_{1}}&{{a}_{2}}\\{{a}_{3}}&{{a}_{4}}\end{array}|$=a1a4-a2a3,若函数f(x)=$|\begin{array}{l}{\sqrt{3}}&{1}\\{cosx}&{sinx}\end{array}|$,将其图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
| A. | $\frac{π}{3}$ | B. | $\frac{2}{3}$π | C. | $\frac{π}{6}$ | D. | $\frac{5}{6}$π |
16.在复平面内,复数z=$\frac{3+4i}{1-i}$对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.设A={0,1,4},B={1,x2},若B⊆A,则x=( )
| A. | 0 | B. | -2 | C. | 0或-2 | D. | 0或±2 |
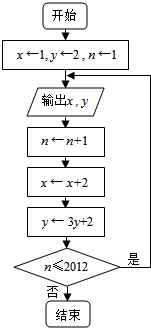 已知数列{xn}、{yn}中的项依次由如图所示的程序框图输出的x,y的值确定.
已知数列{xn}、{yn}中的项依次由如图所示的程序框图输出的x,y的值确定.