题目内容
在ΔABC中,顶点A,B, C所对三边分别是a,b,c已知B(-1, 0), C(1, 0),且b,a, c成等差数列.
(I )求顶点A的轨迹方程;
(II) 设顶点A的轨迹与直线y=kx+m相交于不同的两点M、N,如果存在过点P(0,-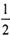 )的直线l,使得点M、N关于l对称,求实数m的取值范围
)的直线l,使得点M、N关于l对称,求实数m的取值范围
(I )求顶点A的轨迹方程;
(II) 设顶点A的轨迹与直线y=kx+m相交于不同的两点M、N,如果存在过点P(0,-
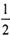 )的直线l,使得点M、N关于l对称,求实数m的取值范围
)的直线l,使得点M、N关于l对称,求实数m的取值范围 (1)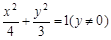 (2)当k=0时,m的取值范围为
(2)当k=0时,m的取值范围为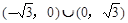 ;
;
当k≠0时,m的取值范围为(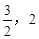 ).
).
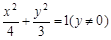 (2)当k=0时,m的取值范围为
(2)当k=0时,m的取值范围为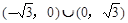 ;
;当k≠0时,m的取值范围为(
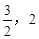 ).
).(I ) 且b,a, c成等差数列结合椭圆的定义求得轨迹方程;(II)将y=kx+m与椭圆方程联立,判别式大于0,根据点关于直线对称,得k、m的关系
解:(I)由题知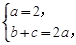 得b+c=4,即|AC|+|AB|=4(定值).
得b+c=4,即|AC|+|AB|=4(定值).
由椭圆定义知,顶点A的轨迹是以B、C为焦点的椭圆(除去左右顶点),
且其长半轴长为2,半焦距为1,于是短半轴长为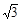 .
.
∴ 顶点A的轨迹方程为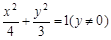 .………………………………4分
.………………………………4分
(II)由
消去y整理得(3+4k2)x2+8kmx+4(m2-3)=0.∴ Δ=(8km)2-4(3+4k2)×4(m2-3)>0,
整理得:4k2>m2-3.①令M(x1,y1),N(x2,y2),则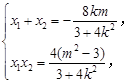
设MN的中点P(x0,y0),则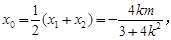
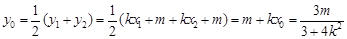 ,…………………7分
,…………………7分
i)当k=0时,由题知,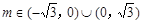 .……………………………8分
.……………………………8分
ii)当k≠0时,直线l方程为 ,由P(x0,y0)在直线l上,得
,由P(x0,y0)在直线l上,得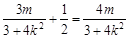 ,得2m=3+4k2.②把②式代入①中可得2m-3>m2-3,解得0<m<2.又由②得2m-3=4k2>0,解得
,得2m=3+4k2.②把②式代入①中可得2m-3>m2-3,解得0<m<2.又由②得2m-3=4k2>0,解得 .∴
.∴  .验证:当(-2,0)在y=kx+m上时,得m=2k代入②得4k2-4k+3=0,k无解.即y=kx+m不会过椭圆左顶点.同理可验证y=kx+m不过右顶点.∴ m的取值范围为(
.验证:当(-2,0)在y=kx+m上时,得m=2k代入②得4k2-4k+3=0,k无解.即y=kx+m不会过椭圆左顶点.同理可验证y=kx+m不过右顶点.∴ m的取值范围为(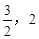 ).………11分
).………11分
综上,当k=0时,m的取值范围为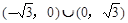 ;当k≠0时,m的取值范围为(
;当k≠0时,m的取值范围为(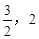 ).
).
解:(I)由题知
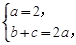 得b+c=4,即|AC|+|AB|=4(定值).
得b+c=4,即|AC|+|AB|=4(定值).由椭圆定义知,顶点A的轨迹是以B、C为焦点的椭圆(除去左右顶点),
且其长半轴长为2,半焦距为1,于是短半轴长为
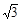 .
.∴ 顶点A的轨迹方程为
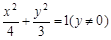 .………………………………4分
.………………………………4分(II)由

消去y整理得(3+4k2)x2+8kmx+4(m2-3)=0.∴ Δ=(8km)2-4(3+4k2)×4(m2-3)>0,
整理得:4k2>m2-3.①令M(x1,y1),N(x2,y2),则
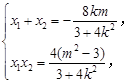
设MN的中点P(x0,y0),则
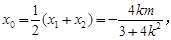
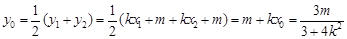 ,…………………7分
,…………………7分i)当k=0时,由题知,
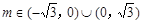 .……………………………8分
.……………………………8分ii)当k≠0时,直线l方程为
 ,由P(x0,y0)在直线l上,得
,由P(x0,y0)在直线l上,得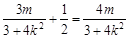 ,得2m=3+4k2.②把②式代入①中可得2m-3>m2-3,解得0<m<2.又由②得2m-3=4k2>0,解得
,得2m=3+4k2.②把②式代入①中可得2m-3>m2-3,解得0<m<2.又由②得2m-3=4k2>0,解得 .∴
.∴  .验证:当(-2,0)在y=kx+m上时,得m=2k代入②得4k2-4k+3=0,k无解.即y=kx+m不会过椭圆左顶点.同理可验证y=kx+m不过右顶点.∴ m的取值范围为(
.验证:当(-2,0)在y=kx+m上时,得m=2k代入②得4k2-4k+3=0,k无解.即y=kx+m不会过椭圆左顶点.同理可验证y=kx+m不过右顶点.∴ m的取值范围为(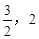 ).………11分
).………11分综上,当k=0时,m的取值范围为
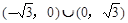 ;当k≠0时,m的取值范围为(
;当k≠0时,m的取值范围为(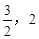 ).
).
练习册系列答案
相关题目
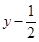 )2=r2(r>0)有一个公共点,且在A处两曲线的切线为同一直线l.
)2=r2(r>0)有一个公共点,且在A处两曲线的切线为同一直线l.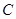 :
: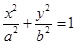
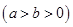 ,称圆心在坐标原点
,称圆心在坐标原点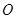 ,半径为
,半径为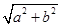 的圆是椭圆
的圆是椭圆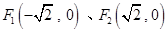 ,椭圆
,椭圆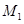 满足
满足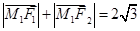 .
.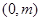
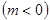 作直线
作直线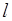 ,使得直线
,使得直线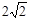 .求出
.求出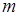 的值.
的值.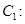
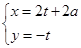 (
(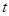 为参数),曲线
为参数),曲线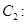
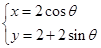 (
(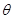 为参数).若曲线
为参数).若曲线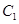 、
、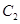 有公共点,则实数
有公共点,则实数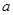 的取值范围_____.
的取值范围_____.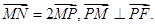
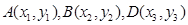 是曲线C上的点,且
是曲线C上的点,且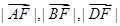 成等差数列,当AD的垂直平分线与x轴交于点E(3,0)时,求点B的坐标。
成等差数列,当AD的垂直平分线与x轴交于点E(3,0)时,求点B的坐标。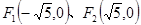 ,直线PF1和PF2相交于点P,且它们的斜率之积为定值
,直线PF1和PF2相交于点P,且它们的斜率之积为定值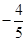 ;
;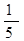 ),N为抛物线C2:
),N为抛物线C2: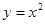 上的一动点,过点N作抛物线C2的切线交曲线C1于P、Q两点,求
上的一动点,过点N作抛物线C2的切线交曲线C1于P、Q两点,求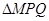 面积的最大值.
面积的最大值.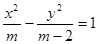 的左焦点与抛物线
的左焦点与抛物线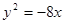 的焦点重合,则
的焦点重合,则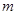 的值为
的值为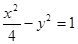 的渐近线与圆
的渐近线与圆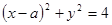 相切,则
相切,则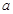 = .
= .