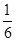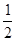题目内容
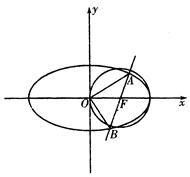
设平面内两定点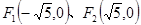 ,直线PF1和PF2相交于点P,且它们的斜率之积为定值
,直线PF1和PF2相交于点P,且它们的斜率之积为定值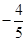 ;
;
(Ⅰ)求动点P的轨迹C1的方程;
(Ⅱ)设M(0,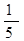 ),N为抛物线C2:
),N为抛物线C2: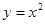 上的一动点,过点N作抛物线C2的切线交曲线C1于P、Q两点,求
上的一动点,过点N作抛物线C2的切线交曲线C1于P、Q两点,求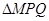 面积的最大值.
面积的最大值.
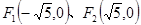 ,直线PF1和PF2相交于点P,且它们的斜率之积为定值
,直线PF1和PF2相交于点P,且它们的斜率之积为定值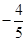 ;
;(Ⅰ)求动点P的轨迹C1的方程;
(Ⅱ)设M(0,
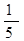 ),N为抛物线C2:
),N为抛物线C2: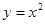 上的一动点,过点N作抛物线C2的切线交曲线C1于P、Q两点,求
上的一动点,过点N作抛物线C2的切线交曲线C1于P、Q两点,求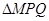 面积的最大值.
面积的最大值.1)设点P(x,y),依题意则有 ,整理得:
,整理得: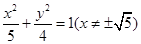
(2)设 ,则PQ的方程为:
,则PQ的方程为: ,联立方程组
,联立方程组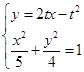 ,
,
消去y整理得:,有 ,
,
而
由 代入化简得:
代入化简得:
即 ;当且仅当
;当且仅当 时,取到最大值。
时,取到最大值。
 ,整理得:
,整理得: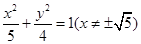
(2)设
 ,则PQ的方程为:
,则PQ的方程为: ,联立方程组
,联立方程组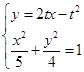 ,
,消去y整理得:,有
 ,
,而

由
 代入化简得:
代入化简得: 即
 ;当且仅当
;当且仅当 时,取到最大值。
时,取到最大值。略

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 过焦点F的直线
过焦点F的直线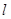 交抛物线于A、B两点,O为原点,若
交抛物线于A、B两点,O为原点,若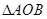 面积最小值为8。
面积最小值为8。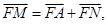 则点M在一定直线上,试证明之。
则点M在一定直线上,试证明之。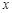 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为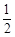 ,且经过点
,且经过点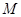
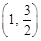 .
.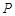 (2,1)的直线
(2,1)的直线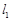 与椭圆
与椭圆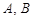 ,满足
,满足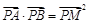 ?若存在,求出直线
?若存在,求出直线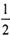 )的直线l,使得点M、N关于l对称,求实数m的取值范围
)的直线l,使得点M、N关于l对称,求实数m的取值范围 ,讨论方程
,讨论方程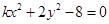 所表示的圆锥曲线类型,并求其焦点坐标
所表示的圆锥曲线类型,并求其焦点坐标 ,点
,点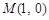 关于
关于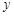 轴的对称点为
轴的对称点为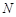 ,直线
,直线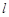 过点
过点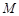 交抛物线于
交抛物线于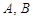 两点.
两点.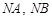 的斜率互为相反数;
的斜率互为相反数; 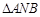 面积的最小值;
面积的最小值;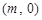 ,
,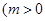 且
且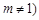 .根据(1)(2)推测并回答下列问题(不必说明理由):①直线
.根据(1)(2)推测并回答下列问题(不必说明理由):①直线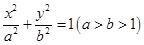 内有圆
内有圆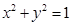 ,如果圆的切线与椭圆交A、B两点,且满足
,如果圆的切线与椭圆交A、B两点,且满足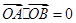 (其中
(其中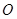 为坐标原点).
为坐标原点).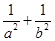 为定值;
为定值;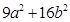 达到最小值,求此时的椭圆方程;
达到最小值,求此时的椭圆方程;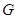 的中心在坐标原点,其中一个焦点为圆
的中心在坐标原点,其中一个焦点为圆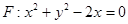 的圆心,右顶点是圆F与x轴的一个交点.已知椭圆
的圆心,右顶点是圆F与x轴的一个交点.已知椭圆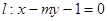 相交于A、B两点.
相交于A、B两点. )求
)求 椭圆的方程;
椭圆的方程;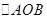 面积的最大值;
面积的最大值;