题目内容
△ABC中，A（-2，0），B（2，0），则满足△ABC的周长为8的点C的轨迹方程为
_______。
_______。
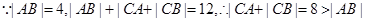.所以点C的轨迹是以A（-2，0），B（2，0）为焦点，长轴长等于8的椭圆，除去长轴的两个端点；a=4,c=2,则
.故点C的轨迹方程为
练习册系列答案
相关题目
.所以点C的轨迹是以A（-2，0），B（2，0）为焦点，长轴长等于8的椭圆，除去长轴的两个端点；a=4,c=2,则.故点C的轨迹方程为题目内容
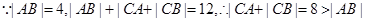.所以点C的轨迹是以A（-2，0），B（2，0）为焦点，长轴长等于8的椭圆，除去长轴的两个端点；a=4,c=2,则.故点C的轨迹方程为
)的直线l,使得点M、N关于l对称，求实数m的取值范围
内有圆
，如果圆的切线与椭圆交A、B两点，且满足
（其中
为坐标原点）．
为定值；
达到最小值，求此时的椭圆方程；
,
，点
满足
，记点
，过点
作直线
与轨迹
两点，过
的垂线
、
，垂足分别为
，记
。
，求证：当
取最小值时，
的面积为
．
的离心率为
，短轴的一个端点到右焦点的距离为2，
求椭圆
的方程；
的直线
与椭圆
、
两点，点
为椭圆
的斜率为
，直线
的斜率为
，试问：
是否为定值？请证明你的结论．
经过椭圆
的左顶点A和上顶点D，椭圆C的右顶点为B，点P是椭圆C上位于
轴上方的动点，直线AP，BP与直线
分别交于M，N两点.
上变化时，讨论S的大小与Q点的个数之间的关系.
的中心在坐标原点，其中一个焦点为圆
的圆心，右顶点是圆F与x轴的一个交点.已知椭圆
相交于A、B两点.
）求
椭圆的方程；
面积的最大值；
轴上,焦距为8,且经过点（0，3）
，问：椭圆C上是否存在一点,使它到直线
的距离最小?最小距离是多少?
