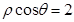题目内容
已知抛物线C:y=(x+1)2与圆M:(x-1)2+(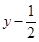 )2=r2(r>0)有一个公共点,且在A处两曲线的切线为同一直线l.
)2=r2(r>0)有一个公共点,且在A处两曲线的切线为同一直线l.
(Ⅰ)求r;
(Ⅱ)设m、n是异于l且与C及M都相切的两条直线,m、n的交点为D,求D到l的距离。
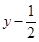 )2=r2(r>0)有一个公共点,且在A处两曲线的切线为同一直线l.
)2=r2(r>0)有一个公共点,且在A处两曲线的切线为同一直线l.(Ⅰ)求r;
(Ⅱ)设m、n是异于l且与C及M都相切的两条直线,m、n的交点为D,求D到l的距离。
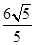
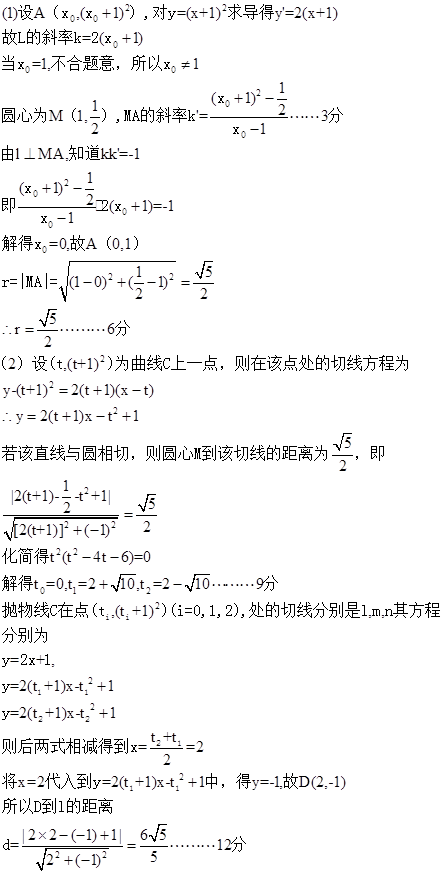
【命题意图】本试题考查了抛物线与圆的方程,以及两个曲线的公共点处的切线的运用,并在此基础上求解点到直线的距离。
【点评】该试题出题的角度不同于平常,因为涉及的是两个二次曲线的交点问题,并且要研究两曲线在公共点出的切线,把解析几何和导数的工具性结合起来,是该试题的创新处。另外对于在第二问中更是难度加大了,出现了另外的两条公共的切线,这样的问题对于我们以后的学习也是一个需要练习的方向。

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 过焦点F的直线
过焦点F的直线 交抛物线于A、B两点,O为原点,若
交抛物线于A、B两点,O为原点,若 面积最小值为8。
面积最小值为8。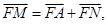 则点M在一定直线上,试证明之。
则点M在一定直线上,试证明之。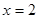 与双曲线C:
与双曲线C: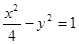 的渐近线交于
的渐近线交于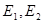 两点,记
两点,记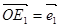 ,
,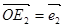 .任取双曲线C上的点
.任取双曲线C上的点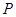 ,若
,若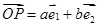 (
(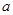 、
、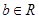 ),则
),则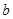 满足的一个等式是 .
满足的一个等式是 .
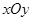 中,已知点
中,已知点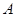
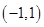 ,P是动点,且三角形
,P是动点,且三角形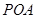 的三边所在直线的斜率满足
的三边所在直线的斜率满足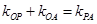 .
.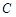 的方程;
的方程;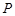 的一个点,且
的一个点,且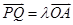 ,直线
,直线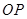 与
与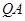 交于点M,试探
交于点M,试探
 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为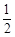 ,且经过点
,且经过点
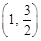 .
. (2,1)的直线
(2,1)的直线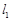 与椭圆
与椭圆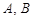 ,满足
,满足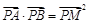 ?若存在,求出直线
?若存在,求出直线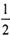 )的直线l,使得点M、N关于l对称,求实数m的取值范围
)的直线l,使得点M、N关于l对称,求实数m的取值范围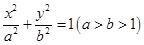 内有圆
内有圆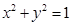 ,如果圆的切线与椭圆交A、B两点,且满足
,如果圆的切线与椭圆交A、B两点,且满足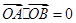 (其中
(其中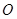 为坐标原点).
为坐标原点).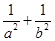 为定值;
为定值;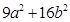 达到最小值,求此时的椭圆方程;
达到最小值,求此时的椭圆方程; 与曲线
与曲线 相切于点
相切于点
 ,则
,则 等于( )
等于( )



 的准线方程是
的准线方程是