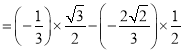Question

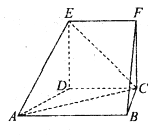
【题目】某地区业余足球运动员共有15000人，其中男运动员9000人，女运动员6000人，为调查该地区业余足球运动员每周平均踢足球占用时间的情况，采用分层抽样的方法，收集300位业务足球运动员每周平均踢足球占用时间的样本数据（单位：小时）
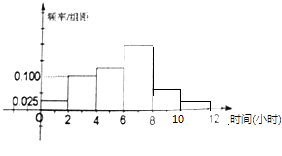
得到业余足球运动员每周平均踢足球所占用时间的频率分布直方图（如图所示），其中样本数据分组区间为：（0，2]，（2，4]，（4，6]，（6，8]，（8，10]，（10，12]．
将“业务运动员的每周平均踢足球时间所占用时间超过4小时”
定义为“热爱足球”．
附：K2=

P（K2≥k0）	0.10	0.05	0.010	0.005
k0	2.706	3.841	6.635	7.879

（1）应收集多少位女运动员样本数据？
（2）估计该地区每周平均踢足球所占用时间超过4个小时的概率．
（3）在样本数据中，有80位女运动员“热爱足球”．请画出“热爱足球与性别”列联表，并判断是否有99%的把握认为“热爱足球与性别有关”．

Answer 1

【答案】
（1）解： ，

∴应收集120位女运动员样本数据

（2）解：由频率分布直方图得1﹣2×（0.100+0.025）=0.75，

∴该地区每周平均踢足球所占用时间超过4个小时的概率的估计值为0.75

（3）解：由（2）知，300位足球运动中有300×0.75=225人的每周平均踢足球时间超过4小时，

75人的每周平均踢足球占用时间超过4小时，

∴热爱足球与性别列联表如下，

	男运动员	女运动员	总计
不热爱足球	35	40	75
热爱足球	145	80	225
总计	180	120	300

结合列联表可算得 = ．

∴有99%的把握认为“热爱足球与性别有关”

【解析】（1）利用分层抽样中每层所抽取的比例数相等求得答案；（2）由频率分布直方图结合概率和为1求得该地区每周平均踢足球所占用时间超过4个小时的概率．（3）由题意列出2×2列联表，计算出k2的值，结合附表得答案．
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识，掌握频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息．