题目内容
【题目】在△ABC中,内角A,B,C对边分别为a,b,c,且c<a,已知 ![]() =﹣2,tanB=2
=﹣2,tanB=2 ![]() ,b=3.
,b=3.
(1)求a和c的值;
(2)求sin(B﹣C)的值.
【答案】
(1)解:∵ ![]() =﹣2,
=﹣2,
∴ ![]() =2,
=2,
∴cacosB=2,
∵tanB=2 ![]() ,
,
∴cosB= ![]() =
= ![]() ,
,
∴ac=2
在△ABC中,由余弦定理得:b2=a2+c2﹣2accosB,
即a2+c2=13,
∴a=2,c=3,或a=3,c=2,
∵a>c,
∴a=3,c=2
(2)解:在△ABC中,sinB=cosBtanB= ![]() ,
,
由正弦定理得sinC= ![]() =
= ![]()
![]() =
= ![]() ,
,
∵a=b>c,
∴C为锐角,
∴cosC= ![]() =
= ![]() ,
,
∴sin(B﹣C)=sinBcosC﹣cosBsinC= ![]() ×
× ![]() +
+ ![]() ×
× ![]() =
= ![]()
【解析】(1)由tanB=2 ![]() 得cosB,由知
得cosB,由知 ![]() ﹣2得accosB=2,解得ac,由余弦定理及a>c,即可解得a,c的值.(2)由(Ⅰ)可求sinB,由正弦定理可求sinC,cosC,利用两角差的正弦函数公式即可得解.
﹣2得accosB=2,解得ac,由余弦定理及a>c,即可解得a,c的值.(2)由(Ⅰ)可求sinB,由正弦定理可求sinC,cosC,利用两角差的正弦函数公式即可得解.

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案【题目】某地区业余足球运动员共有15000人,其中男运动员9000人,女运动员6000人,为调查该地区业余足球运动员每周平均踢足球占用时间的情况,采用分层抽样的方法,收集300位业务足球运动员每周平均踢足球占用时间的样本数据(单位:小时)
得到业余足球运动员每周平均踢足球所占用时间的频率分布直方图(如图所示),其中样本数据分组区间为:(0,2],(2,4],(4,6],(6,8],(8,10],(10,12].
将“业务运动员的每周平均踢足球时间所占用时间超过4小时”
定义为“热爱足球”.
附:K2= ![]()
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
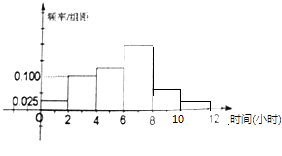
(1)应收集多少位女运动员样本数据?
(2)估计该地区每周平均踢足球所占用时间超过4个小时的概率.
(3)在样本数据中,有80位女运动员“热爱足球”.请画出“热爱足球与性别”列联表,并判断是否有99%的把握认为“热爱足球与性别有关”.