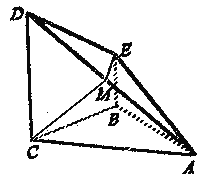
ƒøƒ⁄»ð
°æƒø°ø“—÷™∫Ø ˝![]() £¨
£¨ ![]() .
.
£®1£©«Û∫Ø ˝![]() µƒ◊Ó–°’˝÷Ð∆⁄£ª
µƒ◊Ó–°’˝÷Ð∆⁄£ª
£®2£©»Ù![]() £¨«“
£¨«“![]() £¨«Û
£¨«Û![]() µƒ÷µ.
µƒ÷µ.
°æ¥∞∏°ø(1) ![]() (2)
(2) ![]()
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ:(1)∏˘æð∂˛±∂Ω«π´ Ω∫Õ¡ΩΩ«∫Õ≤Óπ´ Ωµ√µΩ![]() £¨Ω¯∂¯µ√µΩ÷Ð∆⁄£ª£®2£©”…
£¨Ω¯∂¯µ√µΩ÷Ð∆⁄£ª£®2£©”…![]() £¨µ√µΩ
£¨µ√µΩ![]() £¨
£¨ ![]() £¨”…≈‰¥’Ω«π´ Ωµ√µΩ
£¨”…≈‰¥’Ω«π´ Ωµ√µΩ![]() £¨¥˙»Î÷µµ√µΩ∫Ø ˝÷µ.
£¨¥˙»Î÷µµ√µΩ∫Ø ˝÷µ.
Ω‚Œˆ£∫
£®1£©”…“‚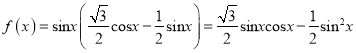
![]() =
=![]()
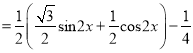
![]()
À˘“‘![]() µƒ◊Ó–°’˝÷Ð∆⁄Œ™
µƒ◊Ó–°’˝÷Ð∆⁄Œ™![]() £ª
£ª
£®2£©”…![]()
![]()
”÷”…![]() µ√
µ√![]() £¨À˘“‘
£¨À˘“‘![]()
π 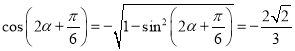 £¨
£¨
π ![]()
![]()
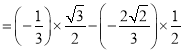
![]()
°æ–հøΩ‚¥Ã‚
°æΩ· ¯°ø
20
°æƒø°øŒ™œÏ”¶ Ææ≈¥Û±®∏Ê÷≥ˆµƒ µ ©œÁ¥Â’Ò–À’Ω¬‘£¨ƒ≥¥Â◊ØÕ∂◊ ![]() ÕÚ‘™Ω®∆¡À“ª◊˘¬Ã…´≈©≤˙∆∑º”π§≥ß.æ≠”™÷–£¨µ⁄“ªƒÍ÷ß≥ˆ
ÕÚ‘™Ω®∆¡À“ª◊˘¬Ã…´≈©≤˙∆∑º”π§≥ß.æ≠”™÷–£¨µ⁄“ªƒÍ÷ß≥ˆ![]() ÕÚ‘™£¨“‘∫Û√øƒÍµƒ÷ß≥ˆ±»…œ“ªƒÍ‘ˆº”¡À
ÕÚ‘™£¨“‘∫Û√øƒÍµƒ÷ß≥ˆ±»…œ“ªƒÍ‘ˆº”¡À![]() ÕÚ‘™£¨¥”µ⁄“ªƒÍ∆√øƒÍ≈©≥°∆∑œ˙ € ’»ÎŒ™
ÕÚ‘™£¨¥”µ⁄“ªƒÍ∆√øƒÍ≈©≥°∆∑œ˙ € ’»ÎŒ™![]() ÕÚ‘™£®«∞
ÕÚ‘™£®«∞![]() ƒÍµƒ¥ø¿˚»Û◊€∫œ=«∞
ƒÍµƒ¥ø¿˚»Û◊€∫œ=«∞![]() ƒÍµƒ ◊Ð ’»Î-«∞
ƒÍµƒ ◊Ð ’»Î-«∞![]() ƒÍµƒ◊Ð÷ß≥ˆ-Õ∂◊ ∂Ó
ƒÍµƒ◊Ð÷ß≥ˆ-Õ∂◊ ∂Ó![]() ÕÚ‘™£©.
ÕÚ‘™£©.
£®1£©∏√≥ߥ”µ⁄º∏ƒÍø™ º”Ø¿˚£ø
£®2£©∏√≥ßµ⁄º∏ƒÍƒÍ∆Ωæ˘¥ø¿˚»Û¥ÔµΩ◊Ó¥Û£ø≤¢«Û≥ˆƒÍ∆Ωæ˘¥ø¿˚»Ûµƒ◊Ó¥Û÷µ.
°æ¥∞∏°ø(1) ¥”µ⁄![]() ø™ º”Ø¿˚(2) ∏√≥ßµ⁄
ø™ º”Ø¿˚(2) ∏√≥ßµ⁄![]() ƒÍƒÍ∆Ωæ˘¥ø¿˚»Û¥ÔµΩ◊Ó¥Û£¨ƒÍ∆Ωæ˘¥ø¿˚»Û◊Ó¥Û÷µŒ™
ƒÍƒÍ∆Ωæ˘¥ø¿˚»Û¥ÔµΩ◊Ó¥Û£¨ƒÍ∆Ωæ˘¥ø¿˚»Û◊Ó¥Û÷µŒ™![]() ÕÚ‘™
ÕÚ‘™
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫(1)∏˘æðπ´ Ωµ√µΩ![]() £¨¡Ó∫Ø ˝÷µ¥Û”⁄0Ω‚µ√≤Œ ˝∑∂Œß£ª£®2£©∏˘æðπ´ Ωµ√µΩ
£¨¡Ó∫Ø ˝÷µ¥Û”⁄0Ω‚µ√≤Œ ˝∑∂Œß£ª£®2£©∏˘æðπ´ Ωµ√µΩ![]() £¨”…æ˘÷µ≤ªµ» Ωµ√µΩ∫Ø ˝◊Ó÷µ.
£¨”…æ˘÷µ≤ªµ» Ωµ√µΩ∫Ø ˝◊Ó÷µ.
Ω‚Œˆ£∫
”…“‚ø…÷™«∞![]() ƒÍµƒ¥ø¿˚»Û◊Ð∫Õ
ƒÍµƒ¥ø¿˚»Û◊Ð∫Õ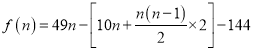
![]()
£®1£©”…![]() £¨º¥
£¨º¥![]() £¨Ω‚µ√
£¨Ω‚µ√![]()
”…![]() ÷™£¨¥”µ⁄
÷™£¨¥”µ⁄![]() ø™ º”Ø¿˚.
ø™ º”Ø¿˚.
£®2£©ƒÍ∆Ωæ˘¥ø¿˚»Û![]()
“ÚŒ™![]() £¨º¥
£¨º¥![]()
À˘“‘![]()
µ±«“Ωˆµ±![]() £¨º¥
£¨º¥![]() ±µ»∫≈≥…¡¢.
±µ»∫≈≥…¡¢.
ƒÍ∆Ωæ˘¥ø¿˚»Û◊Ó¥Û÷µŒ™![]() ÕÚ‘™£¨
ÕÚ‘™£¨
π ∏√≥ßµ⁄![]() ƒÍƒÍ∆Ωæ˘¥ø¿˚»Û¥ÔµΩ◊Ó¥Û£¨ƒÍ∆Ωæ˘¥ø¿˚»Û◊Ó¥Û÷µŒ™
ƒÍƒÍ∆Ωæ˘¥ø¿˚»Û¥ÔµΩ◊Ó¥Û£¨ƒÍ∆Ωæ˘¥ø¿˚»Û◊Ó¥Û÷µŒ™![]() ÕÚ‘™.
ÕÚ‘™.

°æƒø°øƒ≥µÿ«¯“µ”ý◊„«Ú‘À∂Ø‘±π≤”–15000»À£¨∆‰÷–ƒ–‘À∂Ø‘±9000»À£¨≈Æ‘À∂Ø‘±6000»À£¨Œ™µ˜≤È∏√µÿ«¯“µ”ý◊„«Ú‘À∂Ø‘±√ø÷Ð∆Ωæ˘Ãþ◊„«Ú’º”√ ±º‰µƒ«Èøˆ£¨≤…”√∑÷≤„≥È—˘µƒ∑Ω∑®£¨ ’ºØ300Œª“µŒÒ◊„«Ú‘À∂Ø‘±√ø÷Ð∆Ωæ˘Ãþ◊„«Ú’º”√ ±º‰µƒ—˘±æ ˝æ𣮵•Œª£∫–° ±£©
µ√µΩ“µ”ý◊„«Ú‘À∂Ø‘±√ø÷Ð∆Ωæ˘Ãþ◊„«ÚÀ˘’º”√ ±º‰µƒ∆µ¬ ∑÷≤º÷±∑ΩÕº£®»ÁÕºÀ˘ 棩£¨∆‰÷–—˘±æ ˝æð∑÷◊È«¯º‰Œ™£∫£®0£¨2]£¨£®2£¨4]£¨£®4£¨6]£¨£®6£¨8]£¨£®8£¨10]£¨£®10£¨12]£Æ
Ω´°∞“µŒÒ‘À∂Ø‘±µƒ√ø÷Ð∆Ωæ˘Ãþ◊„«Ú ±º‰À˘’º”√ ±º‰≥¨π˝4–° ±°±
∂®“ÂŒ™°∞»»∞Æ◊„«Ú°±£Æ
∏Ω£∫K2= ![]()
P£®K2°ðk0£© | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
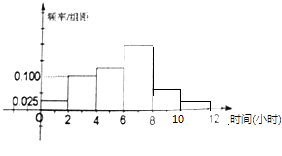
£®1£©”¶ ’ºØ∂ý…ŸŒª≈Æ‘À∂Ø‘±—˘±æ ˝æð£ø
£®2£©π¿º∆∏√µÿ«¯√ø÷Ð∆Ωæ˘Ãþ◊„«ÚÀ˘’º”√ ±º‰≥¨π˝4∏ˆ–° ±µƒ∏≈¬ £Æ
£®3£©‘⁄—˘±æ ˝æð÷–£¨”–80Œª≈Æ‘À∂Ø‘±°∞»»∞Æ◊„«Ú°±£Æ«Îª≠≥ˆ°∞»»∞Æ◊„«Ú”Ζ‘±°±¡–¡™±Ì£¨≤¢≈–∂œ «∑Ò”–99%µƒ∞—Œ’»œŒ™°∞»»∞Æ◊„«Ú”Ζ‘±”–πÿ°±£Æ