题目内容
3.连续抛掷两颗骰子得到的点数分别是a,b,则函数f(x)=ax2-bx在x=1处取得最值的概率是$\frac{1}{12}$.分析 所有的(a,b)共计6×6=36个,函数f(x)=ax2-bx在x=1处取得最值等价于f′(1)=2a-b=0,用列举法求得满足条件的(a,b)有3个,再根据概率公式计算即可.
解答 解:连续抛掷两颗骰子得到的点数分别是a,b,共有36种等可能事件,
∵函数f(x)=ax2-bx在x=1处取得最值,
∴f′(x)=2ax-b,
∴f′(1)=2a-b=0,
即2a=b,
满足的基本事件有(1,2),(2,4),(3,6),共3种,
故函数f(x)=ax2-bx在x=1处取得最值的概率是$\frac{3}{36}$=$\frac{1}{12}$.
故答案为:$\frac{1}{12}$.
点评 本题考主要查古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,列举法,是解决古典概型问题的一种重要的解题方法,属于中档题

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
8.已知实数x∈[1,10]执行如图所示的流程图,则输出的x不小于63的概率为( )
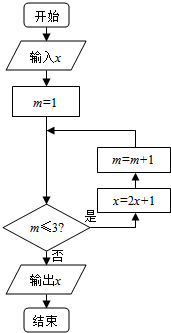

| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{10}$ |
15.若?x∈[$\frac{1}{4}$,+∞),使得不等式ex<$\frac{x-m}{\sqrt{x}}$成立,则实数m的取值范围是( )
| A. | (-∞,-$\frac{1}{2}$${e}^{\frac{1}{4}}$) | B. | ($\frac{1}{4}$-$\frac{1}{2}$${e}^{\frac{1}{4}}$,+∞) | C. | (-∞,$\frac{1}{4}$-$\frac{1}{2}$${e}^{\frac{1}{4}}$) | D. | ($\frac{1}{2}$-$\frac{1}{2}$${e}^{\frac{1}{4}}$,+∞) |
13.函数f(x)=Asin(ωx+θ)(A>0,ω>0)的部分图象如图所示,则f($\frac{π}{3}$)的值为( )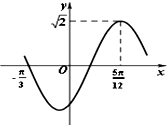

| A. | $\sqrt{2}$ | B. | 0 | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
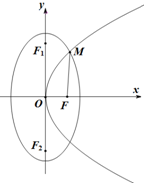 如图,抛物线C1:y2=2px(p>0)与椭圆C2:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{4}$=1(a>2)交于第一象限内一点M,F为抛物线C1的焦点,F1,F2分别为椭圆C2的上下焦点,已知|$\overrightarrow{MF}$-|$\overrightarrow{OF}$|=1,|$\overrightarrow{MF}$-$\overrightarrow{OF}$|=$\sqrt{10}$.
如图,抛物线C1:y2=2px(p>0)与椭圆C2:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{4}$=1(a>2)交于第一象限内一点M,F为抛物线C1的焦点,F1,F2分别为椭圆C2的上下焦点,已知|$\overrightarrow{MF}$-|$\overrightarrow{OF}$|=1,|$\overrightarrow{MF}$-$\overrightarrow{OF}$|=$\sqrt{10}$.