题目内容
5.设集合A=[-2,4),B={x|x2-ax-4≤0},若B⊆A,则实数a的取值范围是[0,3).分析 设f(x)=x2-ax-4,由于△=a2+16>0,由B⊆A,根据区间端点值的关系列式求得a的范围.
解答 解:对于B={x|x2-ax-4≤0},
设f(x)=x2-ax-4,
则△=a2+16>0,
∵B⊆A,集合A=[-2,4),
∴$\left\{\begin{array}{l}{-2<\frac{a}{2}<4}\\{f(-2)≥0}\\{f(4)>0}\end{array}\right.$
解得,0≤a<3,
则实数a的取值范围是[0,3).
故答案为:[0,3).
点评 本题考查了集合的包含关系的应用,考查了分类讨论思想,解答的关键是正确分类,同时根据集合的包含关系分析区间端点值的大小,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.执行如图所示的程序框图,若输出S=15,则框图中①处可以填入 ( )
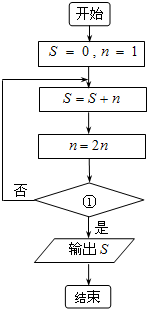

| A. | n≥4? | B. | n≥8? | C. | n≥16? | D. | n<16? |
17.等差数列{an}中,若a4+a8=-3,则a6(a2+2a6+a10)的值是( )
| A. | -9 | B. | 9 | C. | -6 | D. | 3 |
15.若?x∈[$\frac{1}{4}$,+∞),使得不等式ex<$\frac{x-m}{\sqrt{x}}$成立,则实数m的取值范围是( )
| A. | (-∞,-$\frac{1}{2}$${e}^{\frac{1}{4}}$) | B. | ($\frac{1}{4}$-$\frac{1}{2}$${e}^{\frac{1}{4}}$,+∞) | C. | (-∞,$\frac{1}{4}$-$\frac{1}{2}$${e}^{\frac{1}{4}}$) | D. | ($\frac{1}{2}$-$\frac{1}{2}$${e}^{\frac{1}{4}}$,+∞) |
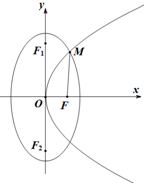 如图,抛物线C1:y2=2px(p>0)与椭圆C2:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{4}$=1(a>2)交于第一象限内一点M,F为抛物线C1的焦点,F1,F2分别为椭圆C2的上下焦点,已知|$\overrightarrow{MF}$-|$\overrightarrow{OF}$|=1,|$\overrightarrow{MF}$-$\overrightarrow{OF}$|=$\sqrt{10}$.
如图,抛物线C1:y2=2px(p>0)与椭圆C2:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{4}$=1(a>2)交于第一象限内一点M,F为抛物线C1的焦点,F1,F2分别为椭圆C2的上下焦点,已知|$\overrightarrow{MF}$-|$\overrightarrow{OF}$|=1,|$\overrightarrow{MF}$-$\overrightarrow{OF}$|=$\sqrt{10}$.