题目内容
9.当a>0时,函数f(x)=(x2+2ax)ex的图象大致是( )| A. | 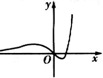 | B. |  | C. | 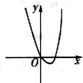 | D. | 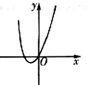 |
分析 用函数的零点,x的变化趋势和f(x)的变化趋势,即可得到答案.
解答 解:由f(x)=0,解得x2+2ax=0,即x=0或x=-2a,
∵a>0,
∴x=-2a<0,
故排除A,C,
当x趋向于-∞时,ex趋向于0,故f(x)趋向于0,排除D.
故选:B.
点评 本题主要考查函数图象的识别和判断,充分利用函数的性质,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
19.某几何体的三视图如图所示(其中侧视图中的圆弧是半圆),则该几何体的表面积为( ) 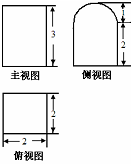

| A. | 20+2π | B. | 20+3π | C. | 24+3π | D. | 24+3π |
20.执行如图所示的程序框图,若输出S=15,则框图中①处可以填入 ( )
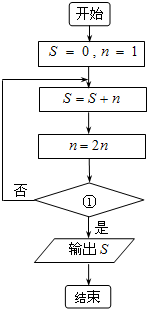

| A. | n≥4? | B. | n≥8? | C. | n≥16? | D. | n<16? |
17.等差数列{an}中,若a4+a8=-3,则a6(a2+2a6+a10)的值是( )
| A. | -9 | B. | 9 | C. | -6 | D. | 3 |
1.已知中心均在原点的椭圆与双曲线有公共焦点,且左、右焦点分别为F1、F2,这两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形.若|PF1|=10,椭圆与双曲线的离心率分别为e1、e2,则e1e2的取值范围为( )
| A. | $({\frac{1}{3},+∞})$ | B. | $({\frac{2}{3},1})$ | C. | (2,+∞) | D. | $({\frac{3}{2},+∞})$ |
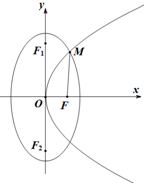 如图,抛物线C1:y2=2px(p>0)与椭圆C2:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{4}$=1(a>2)交于第一象限内一点M,F为抛物线C1的焦点,F1,F2分别为椭圆C2的上下焦点,已知|$\overrightarrow{MF}$-|$\overrightarrow{OF}$|=1,|$\overrightarrow{MF}$-$\overrightarrow{OF}$|=$\sqrt{10}$.
如图,抛物线C1:y2=2px(p>0)与椭圆C2:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{4}$=1(a>2)交于第一象限内一点M,F为抛物线C1的焦点,F1,F2分别为椭圆C2的上下焦点,已知|$\overrightarrow{MF}$-|$\overrightarrow{OF}$|=1,|$\overrightarrow{MF}$-$\overrightarrow{OF}$|=$\sqrt{10}$.