题目内容
设各项均为实数的等比数列{an}的前k项和为Sk,公比q满足:|q|≠1,若S6n=2S4n+11S2n,则
= .
| S10n |
| S8n |
考点:等比数列的性质
专题:计算题,等差数列与等比数列
分析:运用等比数列的求和公式,化简整理,再令q2n=t,则t3-2t2-11t+12=0,解方程求出t=4,再由等比数列的求和公式,化简所求,代入t,即可得到.
解答:
解:由等比数列的求和公式,可得,
S6n=2S4n+11S2n,即为
=2•
+11•
1-q6n=2-2q4n+11-11q2n,
令q2n=t,则t3-2t2-11t+12=0,
即有(t-1)(t2-t-12)=0,
由于|q|≠1,则t≠1,且t>0,
则t=4,S10n=
,S8n=
,
即有
=
=
=
.
故答案为:
.
S6n=2S4n+11S2n,即为
| a1(1-q6n) |
| 1-q |
| a1(1-q4n) |
| 1-q |
| a1(1-q2n) |
| 1-q |
1-q6n=2-2q4n+11-11q2n,
令q2n=t,则t3-2t2-11t+12=0,
即有(t-1)(t2-t-12)=0,
由于|q|≠1,则t≠1,且t>0,
则t=4,S10n=
| a1(1-q10n) |
| 1-q |
| a1(1-q8n) |
| 1-q |
即有
| S10n |
| S8n |
| 1-q10n |
| 1-q8n |
| 1-45 |
| 1-44 |
| 1023 |
| 255 |
故答案为:
| 1023 |
| 255 |
点评:本题考查等比数列的求和公式及运用,考查换元法解题的思想方法,考查运算能力,属于中档题.

练习册系列答案
相关题目
要得到函数y=cos(2x-
)的图象,只需将函数y=cos(2x+
)的图象( )
| 2π |
| 3 |
| π |
| 3 |
A、向右平移
| ||
B、向左平移
| ||
C、向左平移
| ||
D、向右平移
|
 如图,E,F是边长为3的正方形ABCD的边AD上两个点,且AE=DF.连接CF交BD于G,连接BE交AG于点H,若|CH|2:|CE|2=9:10,则AE的长为
如图,E,F是边长为3的正方形ABCD的边AD上两个点,且AE=DF.连接CF交BD于G,连接BE交AG于点H,若|CH|2:|CE|2=9:10,则AE的长为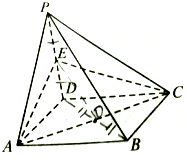 如图,四棱锥P-ABCD的侧面PAD是正三角形,且垂直于底面,底面ABCD是矩形,E是PD的中点,求证:平面ACE⊥平面PCD.
如图,四棱锥P-ABCD的侧面PAD是正三角形,且垂直于底面,底面ABCD是矩形,E是PD的中点,求证:平面ACE⊥平面PCD.