题目内容

要得到函数y=cos（2x-
2π
3
）的图象，只需将函数y=cos（2x+
π
3
）的图象（　　）
A、向右平移
π
3
个单位长度
B、向左平移
π
3
个单位长度
C、向左平移
π
2
个单位长度
D、向右平移
π
2
个单位长度
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：找到两个函数自变量的差别多少，得到平移的方向和大小．
解答： 解：因为y=cos（2x-
2π
3
）=cos[2（x-
π
2
）+
π
3
]，所以要得到函数y=cos（2x-
2π
3
）的图象，只需将函数y=cos（2x+
π
3
）的图象向右平移
π
2
个单位；
故选D．
点评：本题考查了三角函数图象的平移；关键是找到自变量的变化量．
练习册系列答案
相关题目
已知函数f（x）=
x3，x∈(-2，2)
2x，x∈(2，π)
cosx，x∈(π，2π)
，求f（x）在区间（-2，2π）上的定积分．
如图所示，四面体ABCD中，AB⊥BD、AC⊥CD且AD=3，BD=CD=2．
（1）求证：AD⊥BC；
（2）求二面角B-AC-D的余弦值．
设各项均为实数的等比数列{an}的前k项和为Sk，公比q满足：|q|≠1，若S6n=2S4n+11S2n，则
S10n
S8n
=
 
．
向量
a
，
b
，
c
两两夹角为60°，其模为1，则|
a
-
b
|=
 
．
若α+β=
3π
4
，
（1）求（1-tanα）（1-tanβ）的值；
（2）求
tan20°+tan40°+tan120°
tan20°tan40°
的值．
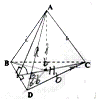如图，已知空间四边形ABCD，及两条对角线AC、BD，AB=AC=AD=a，BD=DC=CD=b，AB⊥面BCD，垂足为H，求平面ABD与平面BCD所成角的大小．
在直角坐标系中，直线l：x-
3
y-2=0被以原点为极点，x轴正半轴的极坐标方程ρ=2cosθ的曲线C所截，则所截得的弦长为
 
．
设抛物线y2=8x上一点P到直线x=-2的距离是6，则点P到该抛物线焦点的距离是（　　）
A、12B、8C、6D、4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网