题目内容
已知二次函数r(x)=ax2-(2a-1)x+b的一个零点是2-
,函数g(x)=lnx,设函数f(x)=r(x)-g(x).
(1)求b的值;
(2)当a>0时,求f(x)的单调增区间.
| 1 |
| a |
(1)求b的值;
(2)当a>0时,求f(x)的单调增区间.
考点:二次函数的性质,函数零点的判定定理
专题:函数的性质及应用,导数的综合应用
分析:(1)由已知条件知,将2-
带入r(x)=0即可求出b=0;
(2)求f′(x)=
,所以解f′(x)≥0即可得出f(x)的单调增区间.
| 1 |
| a |
(2)求f′(x)=
| (2ax+1)(x-1) |
| x |
解答:
解:(1)∵r(x)的一个零点为2-
;
∴r(2-
)=a(2-
)2-(2a-1)(2-
)+b=0;
∴b=0;
(2)f(x)=ax2-(2a-1)x-lnx;
f′(x)=2ax-(2a-1)-
=
=
;
∵a>0,x>0;
∴x≥1时,f′(x)≥0;
∴f(x)在[1,+∞)上单调递增;
即f(x)的单调增区间为[1,+∞);
| 1 |
| a |
∴r(2-
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
∴b=0;
(2)f(x)=ax2-(2a-1)x-lnx;
f′(x)=2ax-(2a-1)-
| 1 |
| x |
| 2ax2-(2a-1)x-1 |
| x |
| (2ax+1)(x-1) |
| x |
∵a>0,x>0;
∴x≥1时,f′(x)≥0;
∴f(x)在[1,+∞)上单调递增;
即f(x)的单调增区间为[1,+∞);
点评:考查函数零点的概念,以及通过解f′(x),解f′(x)≥0得到函数f(x)单调增区间的方法.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
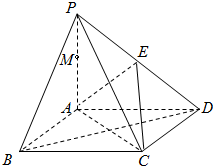 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,BD=4
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,BD=4