题目内容
 如图,E,F是边长为3的正方形ABCD的边AD上两个点,且AE=DF.连接CF交BD于G,连接BE交AG于点H,若|CH|2:|CE|2=9:10,则AE的长为
如图,E,F是边长为3的正方形ABCD的边AD上两个点,且AE=DF.连接CF交BD于G,连接BE交AG于点H,若|CH|2:|CE|2=9:10,则AE的长为考点:相似三角形的性质
专题:立体几何
分析:通过建立直角坐标系,利用直线的方程可得交点G,H的坐标,利用两点之间的距离公式可得|CH|,|CE|,再利用|CH|2:|CE|2=9:10,解出即可.
解答:
解:如图所示, 建立直角坐标系.
建立直角坐标系.
设E(a,3)(0<a<3),则F(3-a,3).
直线BD的方程:y=x,
CF的方程为:y=
(x-3),化为y=-
(x-3),
联立
,解得G(
,
).
直线AG的方程为:y=
x+3,化为y=-
x+3.
直线BE的方程为:y=
x,
联立
,解得H(
,
).
|CH|=
,
|CE|=
.
∵|CH|2:|CE|2=9:10,
∴10[(3-
)2+(
)2]=9[(3-a)2+9]
解得a=1.
∴|AE|=1.
故答案为:1.
 建立直角坐标系.
建立直角坐标系.设E(a,3)(0<a<3),则F(3-a,3).
直线BD的方程:y=x,
CF的方程为:y=
| 3-0 |
| 3-a-3 |
| 3 |
| a |
联立
|
| 9 |
| 3+a |
| 9 |
| 3+a |
直线AG的方程为:y=
3-
| ||
0-
|
| a |
| 3 |
直线BE的方程为:y=
| 3 |
| a |
联立
|
| 9a |
| 9+a2 |
| 27 |
| 9+a2 |
|CH|=
(3-
|
|CE|=
| (3-a)2+9 |
∵|CH|2:|CE|2=9:10,
∴10[(3-
| 9a |
| 9+a2 |
| 27 |
| 9+a2 |
解得a=1.
∴|AE|=1.
故答案为:1.
点评:本题考查了建立直角坐标系利用直线的方程可得交点的坐标、两点之间的距离公式,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
 如图所示,四面体ABCD中,AB⊥BD、AC⊥CD且AD=3,BD=CD=2.
如图所示,四面体ABCD中,AB⊥BD、AC⊥CD且AD=3,BD=CD=2.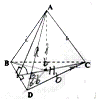 如图,已知空间四边形ABCD,及两条对角线AC、BD,AB=AC=AD=a,BD=DC=CD=b,AB⊥面BCD,垂足为H,求平面ABD与平面BCD所成角的大小.
如图,已知空间四边形ABCD,及两条对角线AC、BD,AB=AC=AD=a,BD=DC=CD=b,AB⊥面BCD,垂足为H,求平面ABD与平面BCD所成角的大小.